Il metodo ipotetico–deduttivo è il processo logico che viene tuttora comunemente utilizzato in ambito scientifico. Dopo l’osservazione di un evento, si procede a formulare una o più ipotesi che possano spiegarne la causa, per poi verificarle sulla base dei dati raccolti nel corso di un esperimento. In questo processo si verifica la validità di un’ipotesi nulla (Hp0), che si contrappone all’ipotesi alternativa di partenza (HpA – talvolta denominata anche Hp1). Per poter rigettare o accettare l’ipotesi nulla con la dovuta accuratezza, è necessario includere un numero di unità statistiche sufficienti.
Questo articolo analizza nel dettaglio la relazione che intercorre tra dimensione campionaria e inferenza statistica, ponendo l’accento sulle implicazioni legate alla potenza del test.
Errore statistico di tipo I e di tipo II
In accordo con il principio di falsificabilità, lo sperimentatore rigetta l’ipotesi nulla in caso di significatività (indicata con α), definita mediante una misura probabilistica specifica, denominata p–value. Il livello di significatività α viene deciso preventivamente dallo sperimentatore e generalmente viene fissato al 5%, con rispettivo p-value pari a 0.05. Ciò significa che lo sperimentatore accetta che sussista un 5% di probabilità di commettere l’errore di rigettare l’ipotesi nulla anche se questa, in realtà, è vera. In termini statistici, tale errore viene definito di tipo I e si contrappone all’errore statistico di tipo II (definito con β), che si verifica quando l’ipotesi nulla – falsa – viene accettata.

Gli errori statistici possono pesare molto sui risultati sperimentali e condurre a conclusioni fuorvianti. Ad esempio, se lo sperimentatore vuole testare la sicurezza di due prodotti, un errore di tipo I (con Hp0: non c’è differenza tra i due prodotti) può portare alla conclusione che i trattamenti differiscano, quando invece tale effetto non sussiste realmente (falso positivo). Al contrario, un errore di tipo II commesso in relazione alla stessa ipotesi può portare alla conclusione che i due prodotti abbiano profili di sicurezza analoghi, quando invece differiscono (falso negativo).
Potenza di un test statistico
L’errore di tipo II misura indirettamente la potenza del test statistico, cioè la probabilità di riuscire a rilevare un effetto quando questo è effettivamente presente. Quanto più elevata è la potenza del test, tanto più si riduce la possibilità di commettere un errore di tipo II.
In effetti, l’errore di tipo I, l’errore di tipo II e la potenza statistica sono tre aspetti intimamente connessi. Si consideri ad esempio una condizione sperimentale in cui si vuole testare l’effetto di un dispositivo medico (DM) rispetto a un placebo (P) sulla base di una variabile (ad es. la persistenza in minuti sulla pelle). L’esperimento potrà essere strutturato per verificare la seguente ipotesi nulla.
- Hp0: i pazienti trattati con il DM NON mostrano una permanenza del prodotto significativamente diversa rispetto ai pazienti trattati con P;
questa si contrappone alla rispettiva ipotesi alternativa:
- HpA: i pazienti trattati con il DM mostrano una permanenza del prodotto significativamente diversa rispetto ai pazienti trattati con P.
Il livello di significatività α viene posto arbitrariamente pari a 5% (p=0.05) e le misure vengono effettuate su 20 pazienti per ciascuna condizione sperimentale.
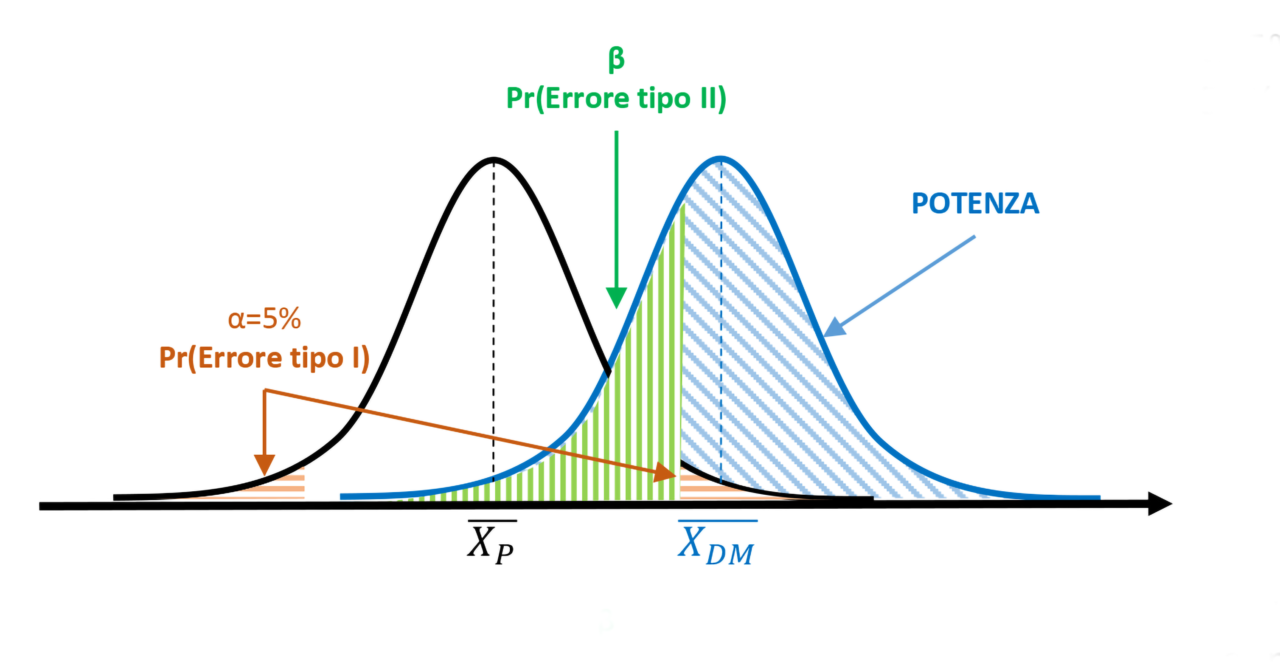
Figura 1. α=5% e potenza del test > 50%
I dati raccolti portano a calcolare un valore statistico superiore al valore critico che delimita l’area di rifiuto pari al 5% (area arancione). L’ipotesi nulla viene quindi rigettata, inferendo che le misure effettuate dopo trattamento con il dispositivo medico appartengono a una popolazione diversa rispetto alle misure ottenute dai soggetti trattati con placebo. In base alla soglia di significatività α, resta una probabilità del 5% di commettere un errore statistico di tipo I. Considerando il grado di sovrapposizione delle due popolazioni, però, è possibile determinare anche il valore di β (area verde), che definisce la probabilità di commettere un errore di tipo II. L’area blu alla destra del limite di β rappresenta la potenza del test (1-β). In questo caso, la potenza copre più della metà dell’area della curva della popolazione DM, risultando superiore al 50%.
Per aumentare la potenza del test e ridurre la probabilità di commettere un errore di tipo II, lo sperimentatore può decidere di allargare la regione di significatività α, ponendola pari a 10%. Tuttavia, così facendo, aumenta la probabilità di commettere un errore di tipo I (10%).
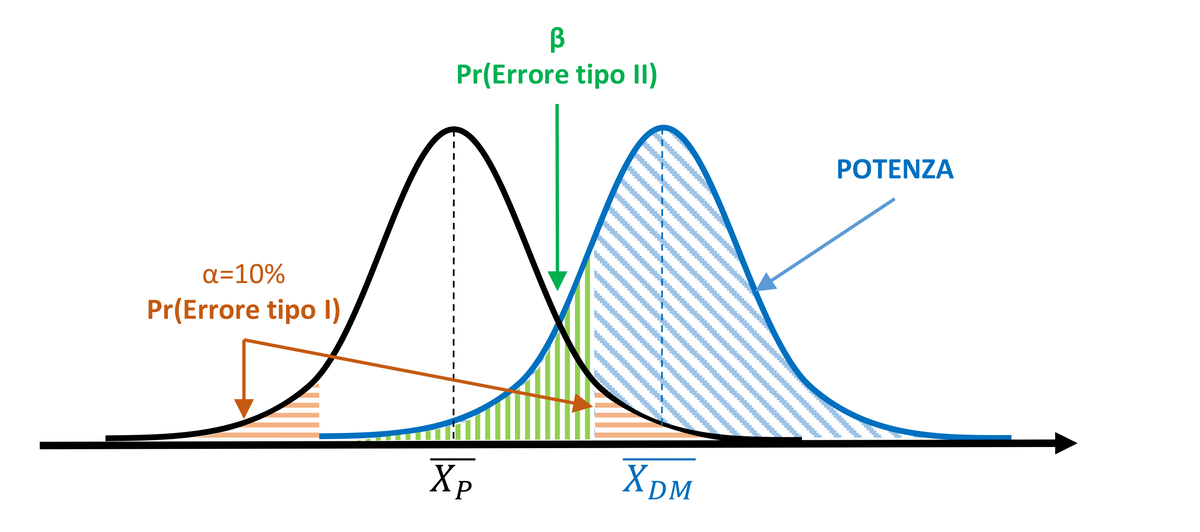
Figura 2. La potenza viene aumentata impostando α=10%, ma la probabilità di errore di tipo I aumenta.
Intuitivamente, a parità di α, la potenza del test aumenterà in funzione dell’effetto del dispositivo medico e in funzione della larghezza della curva (vale a dire in funzione della deviazione standard). Quindi, a parità di deviazione standard, la potenza del test sarà maggiore quanto più la media della popolazione DM si distanzierà rispetto alla media della popolazione P.
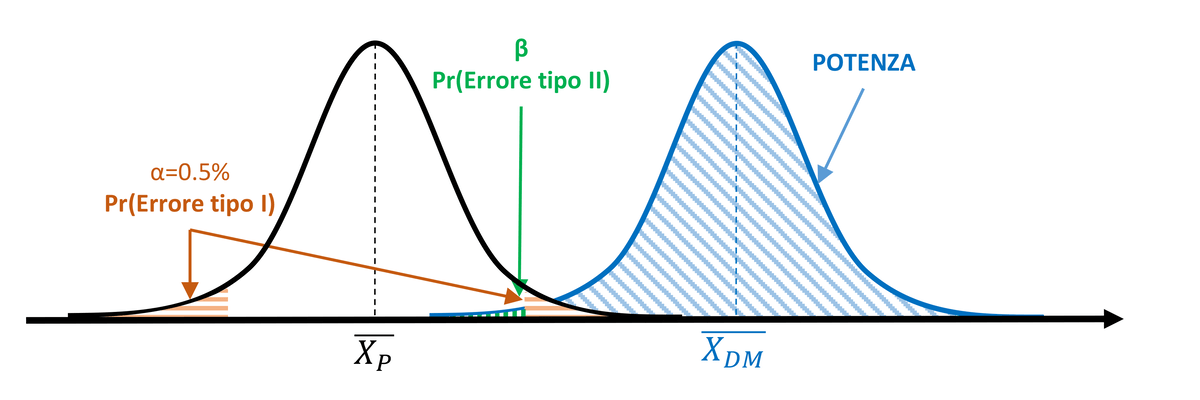
Figura 3. A parità di α (5%) e di deviazione standard σ, la potenza aumenta se la differenza tra le medie è maggiore (l’effetto del trattamento è più marcato).
Analogamente, a parità di distanza tra le medie, la potenza aumenterà in funzione della larghezza della curva e quindi della sua deviazione standard. Infatti, la ridotta dispersione dei valori intorno alla media comporterà anche una riduzione del grado di sovrapposizione delle curve, determinando un incremento nella potenza del test statistico.
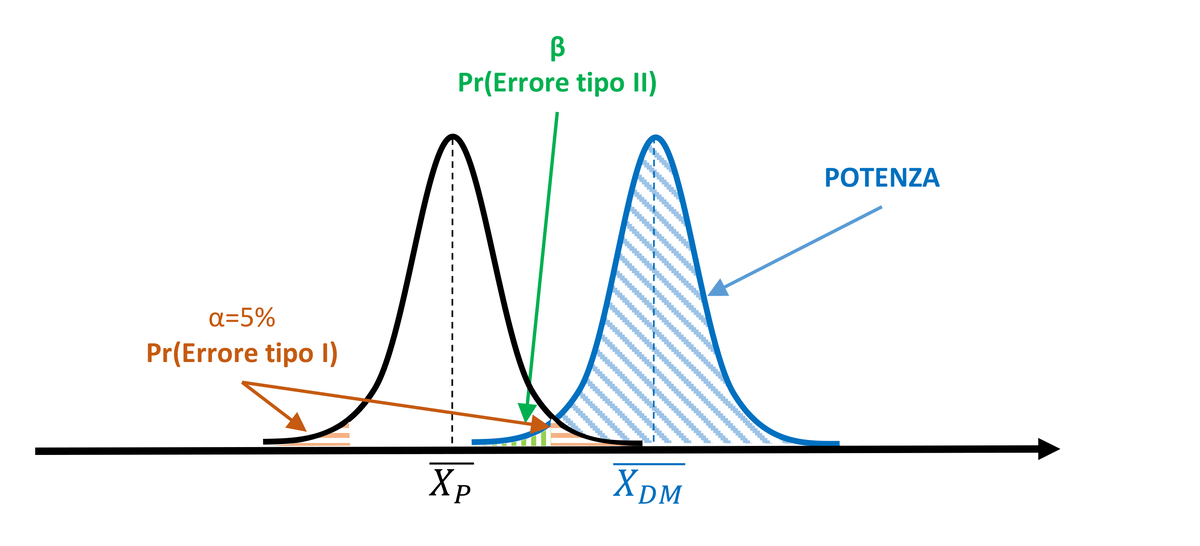
Figura 4. A parità di α (5%) e di differenza tra le medie, la potenza aumenta al diminuire della deviazione standard σ.
La power analysis
A seconda del test statistico, in funzione della probabilità di commettere un errore di tipo I o di tipo II e in relazione alla magnitudo dell’effetto del trattamento indagato, sarà necessario includere un numero diverso di unità sperimentali per poter pervenire a conclusioni ragionevolmente affidabili. In questa fase non si può tralasciare che un numero più elevato di unità statistiche comporta anche uno sforzo sperimentale maggiore, incidendo in modo sostanziale sulle tempistiche e sui costi dell’esperimento, soprattutto in ambito clinico.
Esiste un modo per determinare a priori la numerosità campionaria? La risposta è sì e risiede nella power analysis.
La power analysis è una tecnica analitica basata su quattro parametri strettamente interconnessi:
- Dimensione dell’effetto sperimentale (d)
- Dimensione campionaria (n)
- Significatività (α)
- Potenza statistica (1-β)
La power analysis permette di stimare uno di questi quattro parametri nel momento in cui lo sperimentatore è a conoscenza degli altri tre. Nella maggior parte dei casi, questa tecnica viene applicata a priori (prima di iniziare la fase sperimentale) per calcolare la dimensione campionaria minima (n) per osservare l’effetto di interesse. Mentre la significatività α viene generalmente posta arbitrariamente pari al 5% (0.05) e la potenza statistica pari a 80% (0.8, con β=0.2=20%), la dimensione dell’effetto sperimentale viene calcolata sulla base di dati di letteratura o su stime ragionevolmente proposte dallo sperimentatore. Questo parametro viene calcolato come il rapporto tra la differenza tra le medie (riprendendo l’esempio proposto in precedenza Xdm – Xp), diviso una stima generale delle deviazioni standard, riassumendo in un unico numero (d) il grado di sovrapposizione tra due popolazioni sperimentali. Sulla base di queste considerazioni, si può facilmente intuire che il numero di unità sperimentali necessarie a garantire una potenza pari o superiore a 80% diminuisce all’aumentare della dimensione dell’effetto sperimentale d. In altre parole, se un trattamento è estremamente efficace, basteranno poche misurazioni per rilevare che le misure appartengono a due popolazioni distinte e determinare quindi una significatività statistica. Al contrario, una maggiore dimensione campionaria permetterà di rilevare anche un effetto sperimentale meno marcato. Sarà comunque cura dello sperimentatore interpretare la rilevanza del risultato da un punto di vista clinico.
Conclusione
Un approccio sperimentale poco robusto e strutturato può portare lo sperimentatore a pervenire a conclusioni errate e fuorvianti. La dimensione campionaria incide in modo rilevante sull’accuratezza dell’inferenza statistica, ma deve essere valutata con oculatezza in relazione alle condizioni sperimentali di interesse. La power analysis può essere uno strumento di estrema utilità per definire aprioristicamente il numero di unità sperimentali necessarie a garantire una adeguata potenza statistica.









