L’analisi di sopravvivenza è una metodologia statistica che modella e valuta il tempo che intercorre dall’inizio di un’osservazione al verificarsi di un evento specifico. Nel vasto panorama scientifico, questa analisi si rivela cruciale e nel settore Life Science la sua applicazione assume un ruolo importante.

Pensiamo a domande chiave come:

• “Qual è la prognosi attesa per i pazienti trattati con una nuova terapia?”

• “Esiste una differenza significativa nella sopravvivenza dei pazienti sottoposti a trattamenti diversi?”

• “Quanto tempo impiega un dispositivo medico a raggiungere un punto di malfunzionamento critico?”

Rispondere a questi interrogativi con rigore scientifico è vitale per lo sviluppo di terapie efficaci, la valutazione della sicurezza dei prodotti e la conformità normativa.

La sfida dei dati censurati: perché servono tecniche specifiche

Una peculiarità intrinseca dei dati raccolti per l’analisi di sopravvivenza è la presenza di osservazioni “censurate”. Questi sono casi in cui l’evento di interesse (ad esempio, decesso, recidiva di malattia, guasto del dispositivo) non si è verificato entro la fine dello studio, oppure il soggetto è stato perso al follow-up.

La “censura” non significa che l’evento non accadrà mai, ma semplicemente che non è accaduto entro il periodo di osservazione stabilito. Questo introduce una complessità che richiede l’impiego di tecniche statistiche robuste, capaci di gestire queste informazioni incomplete senza distorcere i risultati dell’analisi.

Lo stimatore di Kaplan-Meier: la soluzione non parametrica

Lo stimatore di Kaplan-Meier emerge come una delle tecniche non parametriche più potenti e diffuse per calcolare la funzione di sopravvivenza in presenza di dati censurati. La funzione di sopravvivenza, indicata come S(t),, rappresenta la probabilità che un individuo “sopravviva” (ovvero, che l’evento non si verifichi) oltre un certo tempo $t$.

Per il calcolo dello stimatore di Kaplan-Meier, si considerano tre elementi chiave:

• t_i: tempi in cui si verifica almeno un evento (morte, guasto, ecc.).
• d_i: numero di eventi al tempo t_i.
• n_i: numero di individui a rischio immediatamente prima del tempo t_i.

La funzione di sopravvivenza stimata al tempo $t$ è data dal prodotto delle probabilità di sopravvivenza a ciascun intervallo di tempo in cui si è verificato un evento.

La curva di Kaplan-Meier: una rappresentazione visiva chiara

La rappresentazione visiva dello stimatore è la curva di Kaplan-Meier: un grafico a gradini intuitivo che illustra l’andamento della probabilità di sopravvivenza nel tempo. Ogni “discesa” verticale nella curva indica un evento osservato (morte, malattia, guasto, ecc.), mentre i segmenti orizzontali mostrano i periodi in cui non si sono verificati eventi. Le osservazioni censurate sono tipicamente contrassegnate sulla curva con simboli specifici, come piccoli trattini verticali. Questa configurazione rende la curva di Kaplan-Meier uno strumento di comunicazione immediato e potente.

Passaggi pratici per un’analisi Kaplan-Meier

Implementare un’analisi di sopravvivenza con il metodo di Kaplan-Meier richiede una serie di passaggi metodologici:

1. raccolta dati: acquisire i dati relativi al tempo di “sopravvivenza” (l’intervallo tra l’inizio dello studio e l’evento o la censura) e lo stato dell’evento (se l’evento si è verificato o se si tratta di censura).

2. organizzazione e ordinamento: organizzare i dati in ordine crescente in base al tempo di sopravvivenza, specificando per ciascun punto temporale se si è verificato un evento o una censura.

3. calcolo della probabilità: calcolare la probabilità di sopravvivenza per ogni tempo in cui si verifica l’evento, seguendo la formula di Kaplan-Meier.

4. costruzione della curva: generare la curva di Kaplan-Meier, ponendo il tempo sull’asse delle ascisse e la probabilità di sopravvivenza sull’asse delle ordinate, indicando gli eventi con segmenti verticali.

5. analisi comparativa (se applicabile): se si desidera confrontare la sopravvivenza tra diversi gruppi (ad esempio, trattamenti diversi), applicare test statistici specifici come il log-rank test o la regressione di Cox.

Esempio pratico: valutazione di trattamenti chirurgici

Consideriamo uno studio ipotetico in cui si valuta la sopravvivenza di 40 pazienti dopo un intervento chirurgico, confrontando un trattamento standard con un nuovo approccio. I dati raccolti potrebbero essere presentati come nel dataset sottostante:

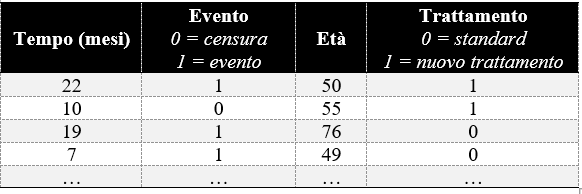
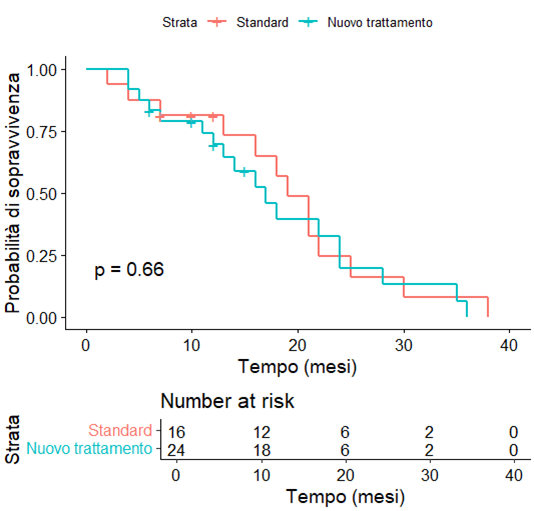
La figura mostra due curve di sopravvivenza caratterizzate da linee a gradini, che si generano inserendo delle linee verticali in corrispondenza del tempo al quale si verificano uno o più eventi (ad es. la morte di un paziente). In base al numero di eventi che si verificano a un determinato tempo, la probabilità di sopravvivenza decade. La tabella sottostante il grafico, invece, indica il numero di soggetti a rischio considerati nell’analisi di sopravvivenza per il calcolo della probabilità, a ciascun tempo, considerando intervalli di 10 anni.

Log-rank test e regressione di Cox: approfondire le differenze

Dopo aver visualizzato le curve di sopravvivenza con Kaplan-Meier, il passo successivo è determinare se le differenze osservate tra i gruppi (ad esempio, tra i diversi trattamenti) siano statisticamente significative.

Il log-rank test è uno strumento statistico primario per questa verifica. La sua ipotesi nulla è che non ci siano differenze significative negli eventi tra le popolazioni studiate in qualsiasi momento. Un valore di probabilità ($p$) basso (<0.05) indicherebbe che le differenze osservate sono probabilmente reali e non dovute al caso. Nell’esempio sopra citato, se il valore di $p$ fosse alto, ciò indicherebbe che non sussistono differenze significative tra i due approcci (standard vs. nuovo trattamento) in termini di sopravvivenza.

Sebbene il log-rank sia già una metodologia informativa sulle differenze tra le popolazioni, non permette allo sperimentatore di analizzare l’influenza di altre variabili sul verificarsi degli eventi, né di quantificare l’entità delle differenze tra i gruppi. A questo scopo, è possibile utilizzare la regressione di Cox, una particolare tecnica di regressione multipla che permette di analizzare il rapporto tra un fattore di rischio e l’incidenza di un determinato esito sperimentale (ad es. morte, guasto, ecc.), correggendo per uno o più fattori di confondimento (ad es. l’età, il sesso, condizioni cliniche specifiche, ecc.).

Conclusione: l’analisi di sopravvivenza come strumento strategico

L’analisi di sopravvivenza, con il metodo di Kaplan-Meier come cardine, è uno strumento statistico potente per chi opera nel settore medico, farmaceutico e dei dispositivi medici. La sua capacità di gestire dati censurati e di permettere confronti tra gruppi, sia visivamente che attraverso test robusti come il log-rank test e la regressione di Cox, offre insight cruciali sulla durata degli eventi.

Comprendere e applicare correttamente queste metodologie non solo migliora la qualità della ricerca e dello sviluppo, ma supporta anche decisioni strategiche fondamentali in ambito clinico e regolatorio.

Per Approfondire:

• Jager KJ, van Dijk PC, Zoccali C, Dekker FW. The analysis of survival data: the Kaplan-Meier method. Kidney Int. 2008 Sep;74(5):560-5. doi: 10.1038/ki.2008.217. Epub 2008 Jul 2. PMID: 18596735.

• Stel VS, Dekker FW, Tripepi G, Zoccali C, Jager KJ. Survival analysis I: the Kaplan-Meier method. Nephron Clin Pract. 2011;119(1):c83-8. doi: 10.1159/000324758. Epub 2011 Jun 15. PMID: 21677442.