Come descritto in un articolo pubblicato in precedenza, una distribuzione normale (o gaussiana) è caratterizzata da una tipica forma a campana, matematicamente definita sulla base di due parametri, la media µ e la deviazione standard σ. In una distribuzione normale, media, moda e mediana coincidono e la distribuzione di frequenza appare simmetrica rispetto al valore centrale, con un’ampiezza variabile in base alla deviazione standard.
Analisi descrittiva per dati non normali
Caratterizzare una distribuzione di dati basandosi esclusivamente sulla media e sulla deviazione standard può essere limitante, in quanto questi parametri non permettono di determinare se le misure seguono un andamento normale. I fattori che ne determinano lo scostamento sono molteplici e includono la presenza di valori anomali (outlier), la sovrapposizione dell’effetto di più fattori, la scarsa accuratezza delle misure, la mancata casualità del campionamento, la presenza di molti valori pari o vicini a 0, l’andamento dei dati secondo una distribuzione diversa dalla gaussiana. Per questo motivo, l’analisi descrittiva deve mirare a comprendere in primo luogo le caratteristiche delle osservazioni, così da poter definire la strategia di analisi più appropriata.
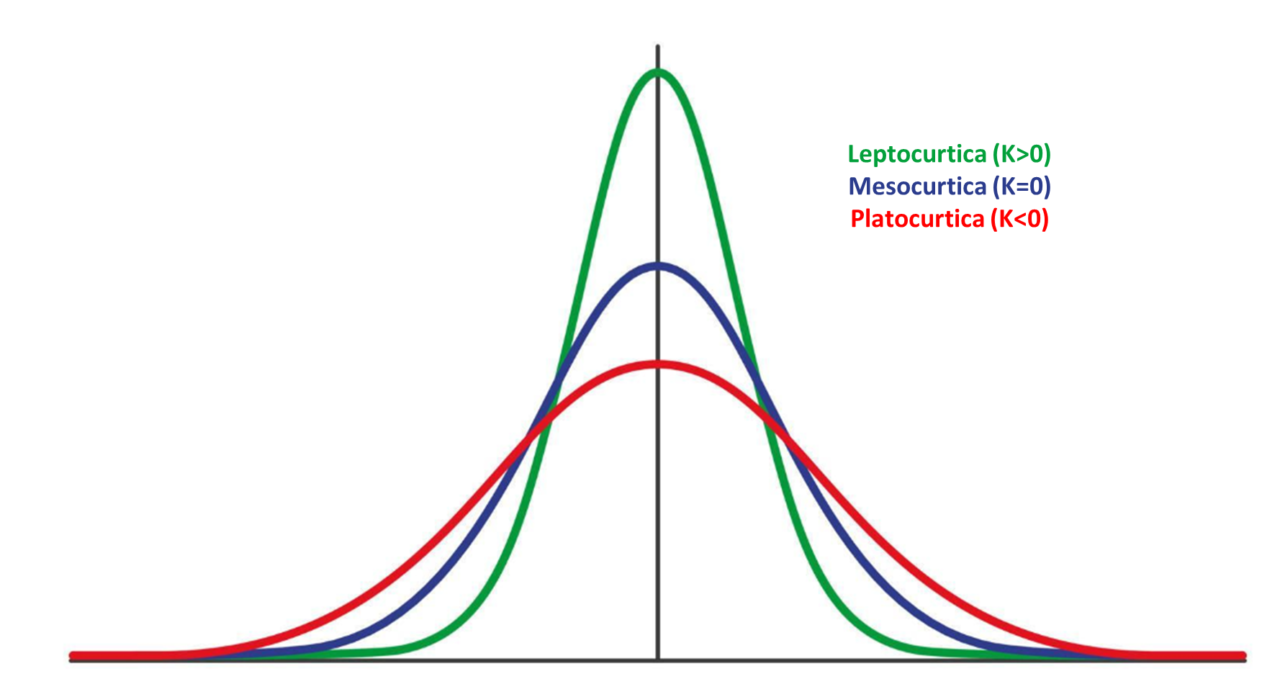
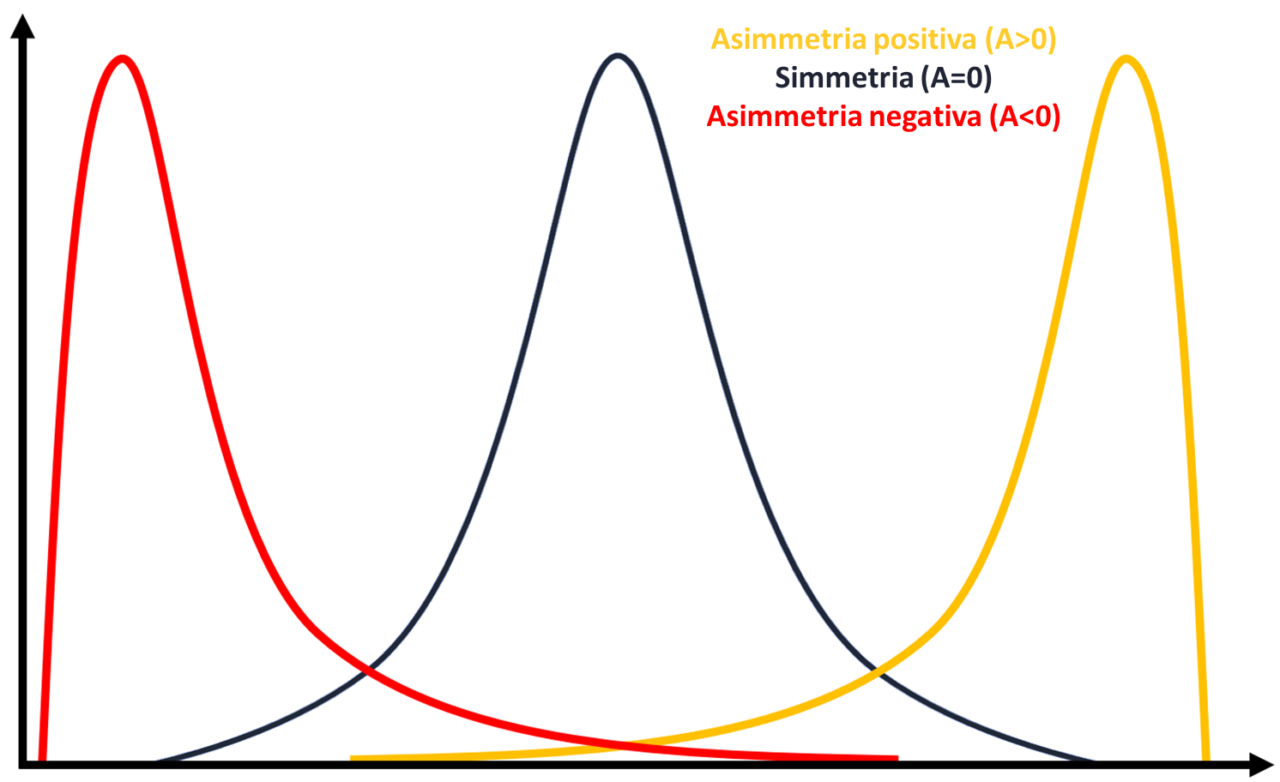
Per valutare se i dati raccolti si distribuiscono normalmente, si può ricorrere a metodi grafici (istogrammi, q-q plot) o statistici (test di Shapiro-Wilk o test di Kolmogorov-Smirnov). Inoltre, esistono degli indici descrittivi che permettono di caratterizzare in modo più dettagliato la distribuzione di un insieme di dati. Questi includono la curtosi e l’asimmetria (o skewness). La curtosi, espressa mediante l’indice K, definisce quanto la curva è “appuntita” rispetto a una distribuzione normale (K=0 definisce una forma mesocurtica; K>0 definisce una forma leptocurtica; K<0 definisce una forma platicurtica). La simmetria, invece, viene generalmente espressa mediante l’indice A, che assume valori positivi (A>0) per distribuzioni in cui le osservazioni si raggruppano nella regione con valori più bassi (asimmetria a destra, con una lunga coda verso i valori maggiori) e valori negativi (A<0) per distribuzioni in cui la coda è spostata a sinistra.
Per comprendere meglio quanto descritto, si considerino, ad esempio, le misure del peso di 10 unità statistiche sottoposte a due condizioni sperimentali distinte (A e B), dalle quali si ottiene una media(A)=76,7 kg e media(B)=87,3 kg.
A: 50, 66, 85, 90, 77, 78, 79, 77, 65, 100 – media: 76,7±13,98
B: 74, 50, 97, 90, 63, 81, 72, 60, 65, 221 – media: 87,3±49,05
Una prima analisi superficiale potrebbe portare a concludere che le unità statistiche misurate nella condizione sperimentale B sono caratterizzate da un peso mediamente più elevato e che, potenzialmente, questa misura possa essere determinata dalla condizione sperimentale a cui esse afferiscono. Tuttavia, un’analisi più attenta evidenzia una forte asimmetria nella distribuzione dei dati misurati per la condizione B (asimmetria=2,69), in relazione alla presenza di un valore anomalo, pari a 221 kg.
Come comportarsi in questi casi? Sicuramente, si può essere tentati di rimuovere il valore anomalo dalla serie di dati, così da eliminare l’elemento che determina l’asimmetria della distribuzione. Un simile approccio, però, può essere applicato solo se lo sperimentatore è consapevole che tale misura deriva da un errore tecnico palese, come il malfunzionamento dello strumento di misura, una variazione nella tecnica di misurazione, ecc. In caso contrario, il valore di 221 kg rappresenterà un elemento che descrive una variabilità intrinseca delle unità statistiche afferenti alla condizione B, suggerendo, potenzialmente, che l’esperimento dovrebbe includere un maggiore numero di repliche (n) per poter cogliere al meglio la variabilità del fenomeno misurato.
In tali occasioni, lo sperimentatore può basare le analisi descrittive sulla mediana, che diversamente dalla media è meno influenzata dai valori estremi. In riferimento all’esempio sopra riportato, la mediana delle misure per la condizione A è pari a 77,5 kg, mentre quella per la condizione B è pari a 73 kg! Ugualmente, al posto della deviazione standard, la dispersione dei valori può essere espressa in termini di range interquartile (A: 14,75; B: 24,25).
Analisi inferenziale per dati non normali
L’applicazione di test statistici è sempre un passaggio delicato, che è necessario approcciare con consapevolezza. Per esempio, la condizione di normalità è un prerequisito fondamentale per l’applicazione di test statistici parametrici (come ad es. il test ANOVA, il t-test, il test di correlazione di Pearson, l’analisi di regressione lineare). Se i dati non rispettano tale caratteristica, l’esito del test rischia di condurre a un’inferenza statica fuorviante.
Quando i dati non si distribuiscono in modo normale, un primo approccio è quello di trasformarli sulla base della radice quadrata o del logaritmo prima di condurre il test, così da favorire l’approssimazione dei dati a una gaussiana. Qualora, a seguito di tale trasformazione, i dati si distribuissero in modo normale, sarà possibile ricorrere all’applicazione di test statistici parametrici. Se al contrario la trasformazione risultasse inefficace, lo sperimentatore ha la possibilità di utilizzare test statistici non parametrici, che non implicano alcuna assunzione sulla distribuzione di base delle variabili. Ad esempio, il test dei segni per ranghi di Wilcoxon (Wilcoxon signed rank test) può essere utilizzato come corrispondente non parametrica del t-test, il test di Kruskal-Wallis come corrispondente non parametrica dell’analisi ANOVA e il test di correlazione di Spearman come corrispondente non parametrico della correlazione di Pearson.
La distribuzione di frequenza di una variabile viene influenzata da molteplici fattori. In un’indagine scientifica, è fondamentale comprendere tale distribuzione per definire il processo di analisi più appropriato. Quando i dati non seguono un andamento normale, lo sperimentatore può decidere di applicare test statistici non parametrici, svicolati da alcuni assunti di base dei test parametrici.