La distribuzione normale è la distribuzione di frequenza più diffusa e maggiormente nota in ambito statistico. Essa, infatti, permette di descrivere la maggior parte dei fenomeni naturali osservabili attraverso caratteri quantitativi, per i quali, all’aumentare delle misurazioni, la distribuzione di frequenza tenderà ad assumere sempre di più la caratteristica forma a campana di una distribuzione normale.
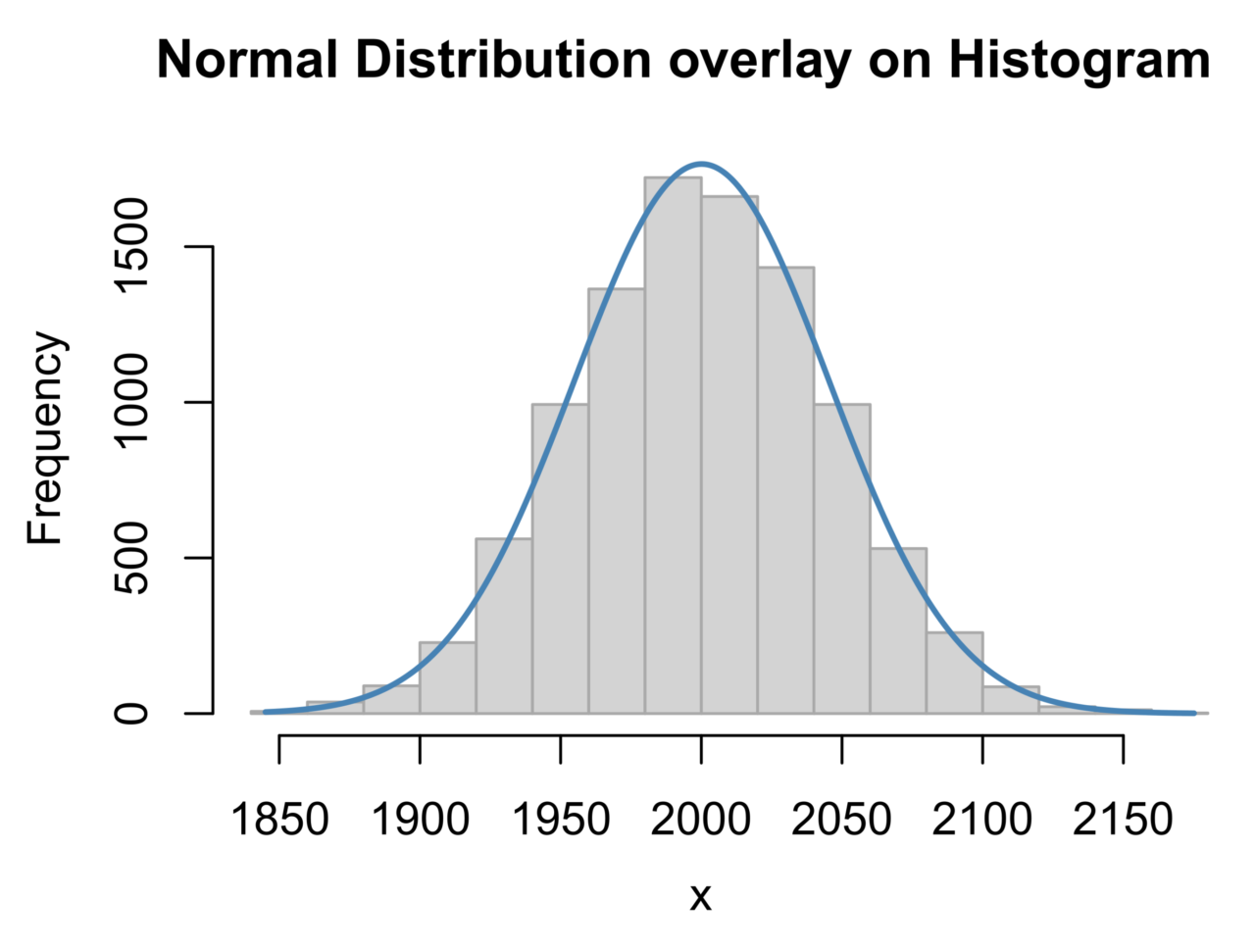
Se si osserva l’immagine riportata di seguito – che raffigura una distribuzione normale ottenuta sulla base della frequenza delle misurazioni di una ipotetica variabile x – si nota che la curva è caratterizzata da un unico picco di frequenza e che è perfettamente simmetrica ai due margini del valore centrale. Intuitivamente, ciò implica che i valori centrali sono le misure della variabile x osservate con maggiore frequenza, mentre i valori che si distribuiscono ai limiti superiori e inferiori della curva sono quelli osservati più raramente.
Ma perché per una stessa variabile si osservano misure diverse e perché queste misure si distribuiscono secondo una curva normale? La risposta alla prima domanda risiede nel fatto che diverse misurazioni di una stessa variabile – effettuate su più unità statistiche – possono derivare da errori di misurazione, dovuti per esempio allo strumento, all’abilità tecnica dello sperimentatore, alla variabilità intrinseca delle unità statistiche o a una variabilità sperimentale dovuta a fattori che non possono essere tenuti sotto controllo. Per questo motivo la distribuzione normale viene anche definita come la curva degli errori accidentali. In merito al secondo quesito, è necessario fare riferimento al teorema del limite centrale, che afferma che la somma (o la media) di un grande numero di variabili aleatorie indipendenti e dotate della stessa distribuzione è approssimativamente normale, indipendentemente dalla distribuzione soggiacente. Ciò significa che, all’aumentare della dimensione campionaria, lo sperimentatore può determinare sempre più accuratamente la distribuzione di alcune statistiche – ad es. la media – anche se non ha alcuna informazione sulla distribuzione della popolazione da cui sono stati ottenuti i campioni.
Caratteristiche della distribuzione normale
In una distribuzione normale, il valore centrale corrisponde esattamente alla media, alla mediana e alla moda della serie di dati – per una descrizione più approfondita di media, mediana e moda, puoi leggere questo articolo. Ciò implica che in una distribuzione normale la percentuale delle osservazioni si distribuisce uniformemente ai due lati del valore centrale, il 50% sarà a sinistra della media e la restante metà sarà a destra. Tuttavia, il valore centrale da solo non basta a descrivere una distribuzione normale. Un altro parametro fondamentale è la deviazione standard, che misura la dispersione delle osservazioni rispetto al valore centrale. Tale variabilità modifica l’ampiezza della curva e quindi la frequenza con la quale si osservano misure che si discostano dal valore medio.
Anche se può apparire complessa, la funzione che descrive una distribuzione normale è basata su questi due parametri, la media µ e la deviazione standard σ:
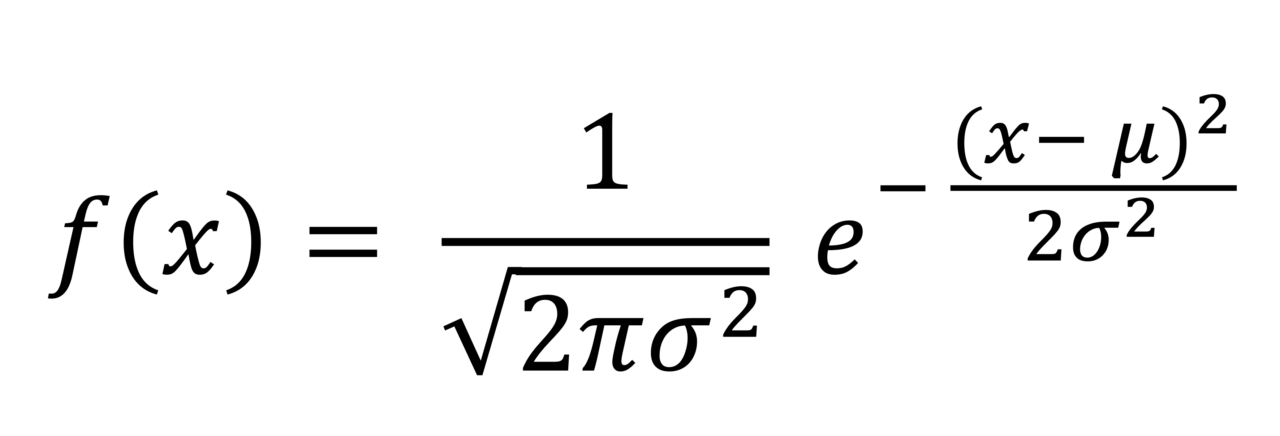
Modificando il valore di uno dei due, si otterranno distribuzioni di frequenza normale differenti. Se varia la media e non la deviazione standard, la curva manterrà la medesima forma, ma apparirà traslata sull’asse delle x. Se varia la deviazione standard e la media rimane inalterata, la curva manterrà lo stesso valore centrale sull’asse delle x, ma varierà in ampiezza e, a parità del numero di osservazioni, risulterà più piatta (varia cioè la frequenza delle osservazioni in prossimità del valore centrale).
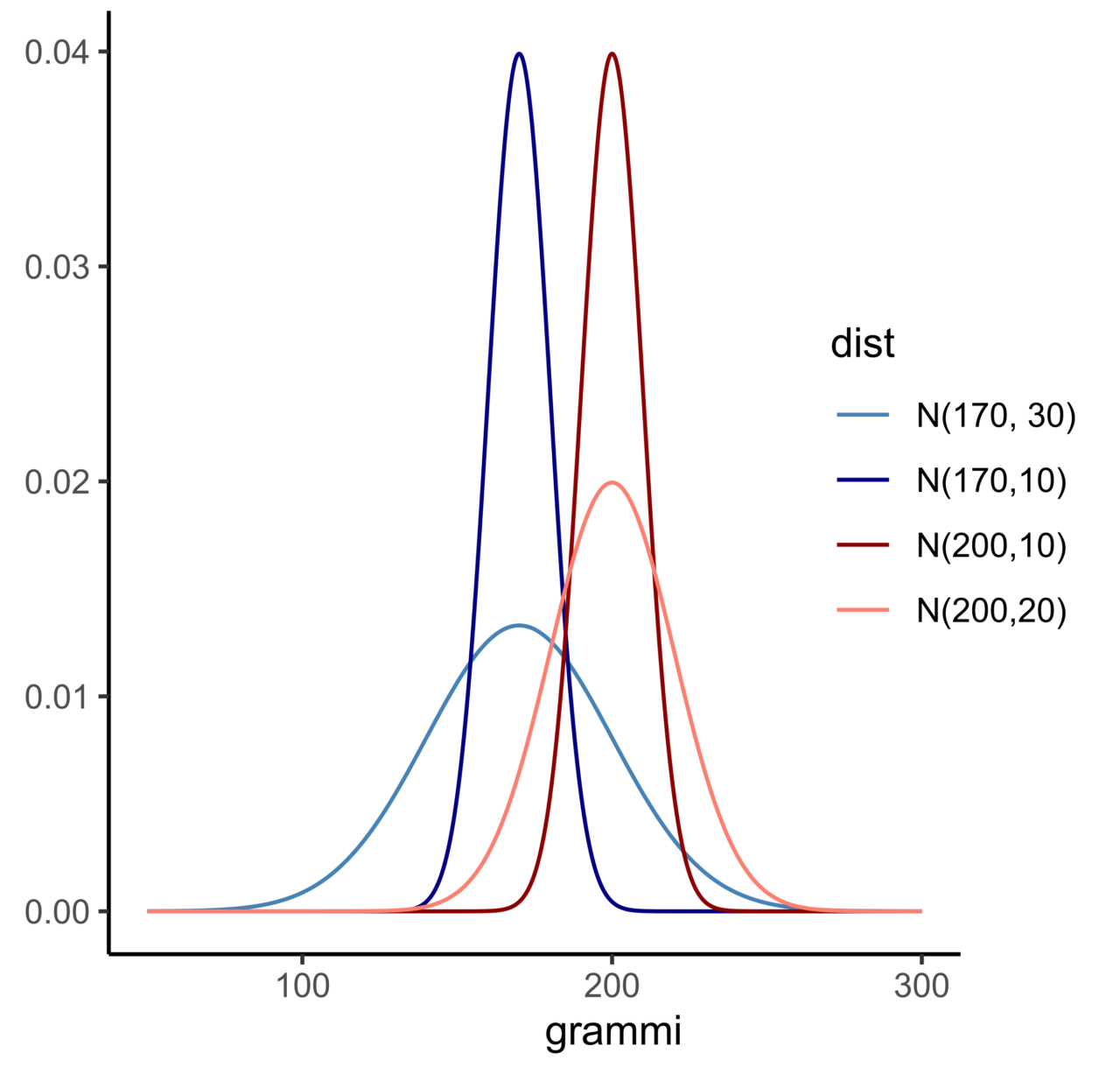
Queste variazioni appaiono chiare se si osserva il grafico riportato di seguito, che rappresenta un esempio di distribuzioni normali relative alle misure del peso di un ipotetico oggetto. Si può notare come le distribuzioni indicate in blu/azzurro – N(170, 10)/N(170, 30), dove “N” indica la distribuzione normale, il primo numero la media e il secondo la deviazione standard – hanno la stessa media (170 grammi), ma diversa deviazione standard (10 e 30, rispettivamente). Ciò si traduce in uno stesso posizionamento del valore centrale sull’asse delle ascisse, ma in una diversa ampiezza della curva. Le distribuzioni normali indicate in rosso/rosa – N(200, 10)/N(200, 20) – hanno anch’esse uguale media e diversa deviazione standard, ma presentano un valore medio più elevato rispetto alle curve blu/azzurra e quindi si posizionano più a destra rispetto a queste ultime.
Come riconoscere una distribuzione normale
In base quanto descritto, è facile comprendere come sia estremamente rilevante riuscire a capire se le osservazioni raccolte si distribuiscono normalmente o meno. A questo scopo, lo sperimentatore può fare ricorso a metodi grafici e statistici.
Graficamente, è possibile verificare la normalità mediante un istogramma, che deve risultare simmetrico e senza valori anomali (outlier) evidenti. Tra gli strumenti grafici più noti e utilizzati, c’è anche il così detto q-q plot, cioè il grafico dei quantili. Questo consiste in un grafico a dispersione che permette di confrontare i quantili di una distribuzione normale con i quantili della variabile osservata. Se quest’ultima segue un andamento normale, nel q-q plot i valori si distribuiranno lungo la diagonale.
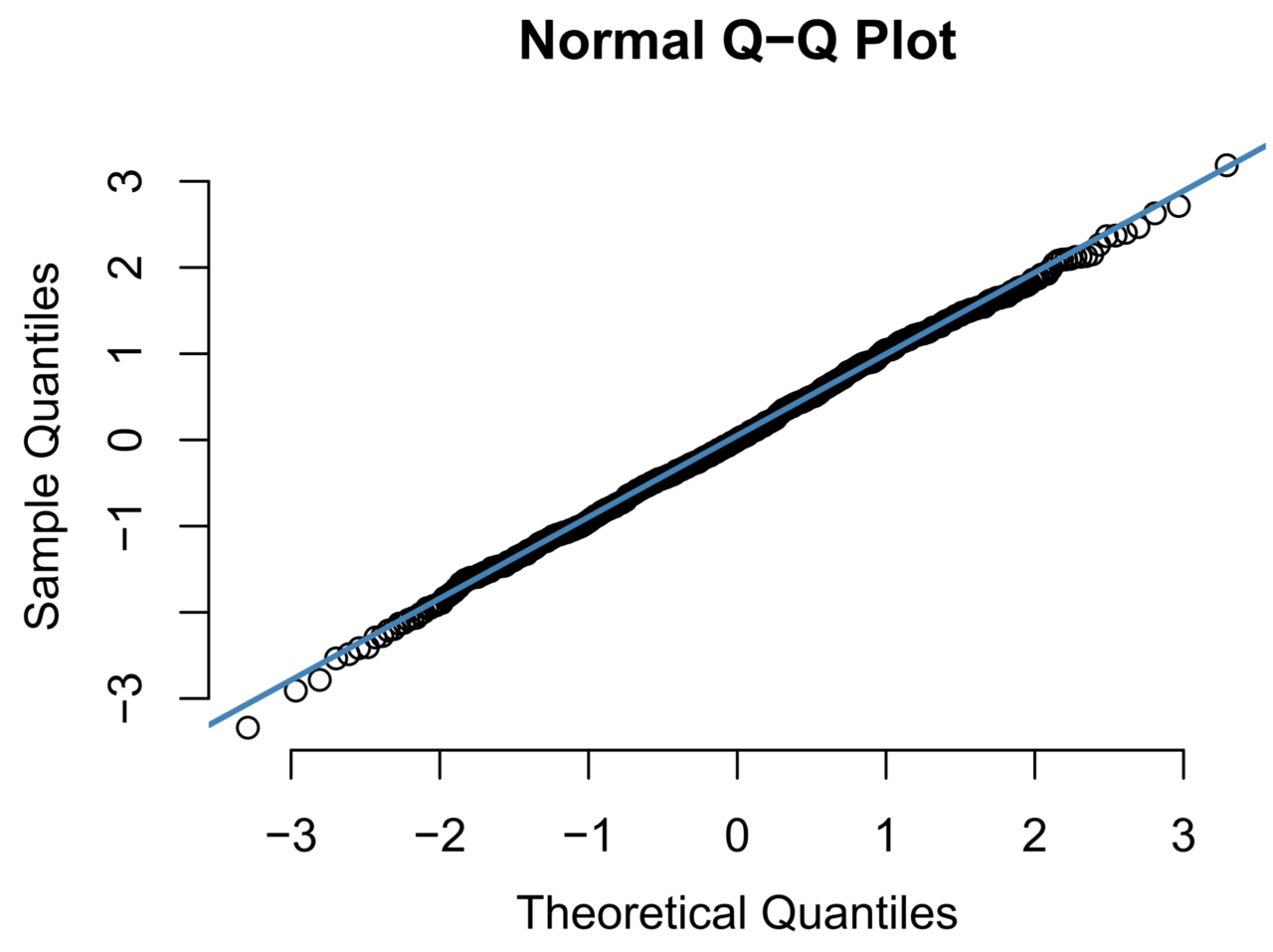
Se da un lato i metodi grafici sono molto efficaci per raccogliere velocemente e in maniera intuitiva l’informazione circa la normalità dei dati, è possibile procedere anche con un approccio quantitativo, basato su specifici test statistici. I test di normalità più noti e utilizzati sono il test di Shapiro-Wilk e il test di Kolmogorov-Smirnov (quest’ultimo particolarmente indicato per campioni ad elevata numerosità).
Solitamente, la normalità dei grafici viene verificata sia quantitativamente mediante test statistici sia graficamente con il supporto di istogrammi e q-q plot.
Distribuzione normale – implicazioni statistiche
Un’implicazione importante in ambito statistico legata al concetto di normalità è che l’area sottesa alla curva che definisce la distribuzione normale descrive la probabilità del verificarsi di un evento. Il totale dell’area è 1, cioè il 100% delle osservazioni. Allora, ipotizzando di prendere come riferimento un determinato valore della variabile misurata, sarà possibile calcolare la probabilità di ottenere un valore inferiore o inferiore a quello di riferimento. In relazione a questo principio, quando i dati si distribuiscono normalmente, sarà possibile effettuare analisi statistiche inferenziali basate su test parametrici. Se, al contrario, la variabile misurata presenta una distribuzione che differisce rispetto all’andamento normale, sarà necessario ricorrere a test statistici non parametrici.
Saper riconoscere quando i dati assumono una distribuzione normale è di fondamentale importanza per poter decidere quale sia l’approccio statistico più indicato all’analisi dei dati raccolti. I risultati ottenuti da test statistici parametrici applicati a dati che non si distribuiscono normalmente possono risultare fuorvianti, determinare errori inferenziali e condurre lo sperimentatore a conclusioni non veritiere.