In un precedente articolo sono stati riassunti alcuni concetti statistici di base che possono essere di supporto per analizzare con maggiore consapevolezza i dati sperimentali raccolti nel corso di un’investigazione scientifica. Dopo aver sinteticamente distinto statistica descrittiva e inferenziale, venivano sintetizzati alcuni punti chiave in ambito sperimentale e si classificavano i caratteri (qualitativi e quantitativi) tramite i quali si possono descrivere le unità statistiche.
Nell’ambito della statistica descrittiva, è possibile caratterizzare la distribuzione di un insieme di dati mediante la stima di alcuni indici di riferimento. In generale, si distinguono tre categorie di indici statistici: gli indici di posizione, gli indici di dispersione e gli indici di forma. Gli indici di posizione maggiormente utilizzati sono la media, la moda e la mediana, che vengono stimati per definire la tendenza centrale del campione o della popolazione statistica.
Media
La media è quel singolo valore numerico che descrive sinteticamente una distribuzione di dati e che è compreso tra il valore minimo e il valore massimo di tale distribuzione. In realtà si possono distinguere diversi tipi di medie in relazione alla formula matematica utilizzata per calcolarle, ma in questo breve articolo verrà presa specificatamente in esame la media aritmetica, che è probabilmente il valore più diffuso nell’ambito della statistica descrittiva. Quando ci troviamo ad analizzare un carattere quantitativo misurato su più unità statistiche, la media aritmetica è il valore numerico ottenuto dividendo la somma di tutti i valori a disposizione per il numero totale delle osservazioni. Più nello specifico, la media aritmetica rappresenta il valore che, sostituito a ciascun xi (esito di ogni i-esima misura) nella definizione della media, lascia invariata l’espressione della media stessa.
Mediana
La mediana è un indice differente rispetto alla media, perché rappresenta quel valore che ripartisce la distribuzione in due metà. La prima metà conterrà tutti i valori inferiori o uguali alla mediana, mentre la seconda metà conterrà tutti i valori uguali o maggiori alla mediana. In virtù di tali caratteristiche, la mediana rappresenta quel valore per il quale la frequenza relativa cumulata è pari allo 0.5 (50%). Operativamente, ipotizzando di aver misurato una stessa variabile su diverse unità statistiche, la mediana si identifica dopo aver disposto i valori in ordine crescente. Se il numero delle osservazioni è dispari, la mediana corrisponde al valore centrale che divide la distribuzione in due metà; se il numero delle osservazioni è pari, la mediana è il valore corrispondente alla media aritmetica calcolata considerando i due valori centrali della distribuzione. Un aspetto rilevante è che, rispetto alla media, la mediana è meno sensibile alla presenza di valori anomali (outlier) – cioè misure insolitamente elevate e/o insolitamente basse.
Moda
Diversamente dalla media e dalla mediana, la moda viene generalmente espressa nell’analisi di dati qualitativi o di variabili discrete. La moda – detta anche norma – di una distribuzione si identifica con quella modalità del carattere che compare più frequentemente. Quando la moda si identifica in una singola modalità di un carattere, la distribuzione viene definita unimodale, mentre picchi di frequenza relativi a due o più modalità definiscono distribuzioni bimodali o plurimodali.
Esempi pratici
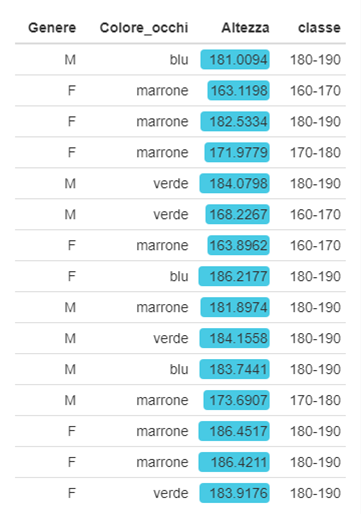
Per offrire una prospettiva più concreta sulla reale applicabilità di questi concetti e sulle informazioni che se ne possono trarre, verrà qui presentato un semplice esempio di calcolo. Si consideri un set di dati che descrive il sesso, il colore degli occhi e l’altezza (in cm) di 15 soggetti. Sesso e colore degli occhi sono caratteri qualitativi nominali, mentre la misura dell’altezza è una variabile continua.
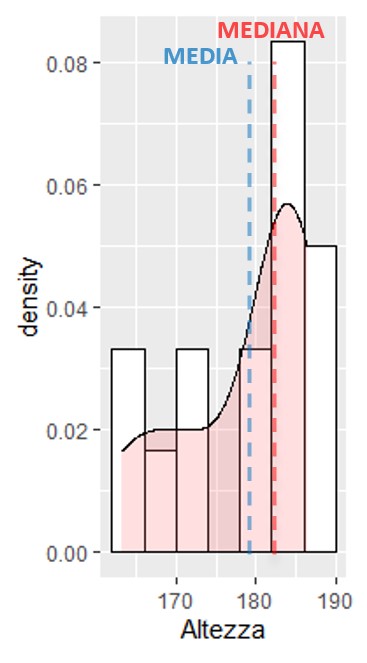
In questo caso, media e mediana potranno essere stimate esclusivamente in relazione alla variabile continua (altezza). La media aritmetica corrisponderà alla somma di tutti i valori misurati (2681.34 cm) diviso il numero di osservazioni (N=15): 178.756 cm. La mediana, invece, viene identificata come quel valore che divide la distribuzione in due metà, dopo aver disposto le misure di altezza in ordine crescente: 182.53 cm (seconda osservazione in tabella). Per quanto riguarda l’altezza, è evidente che le misure sono tutte differenti e quindi non è possibile identificare la moda con un valore specifico. Se però le misure di altezza vengono raggruppate in classi di 10 cm, si osserva che la moda si esprime per la classe 180–190 cm…questo esperimento è stato condotto probabilmente nel Nord Europa!
Sulla base del valore assunto da media, moda e mediana, è possibile dedurre la struttura della distribuzione statistica oggetto di analisi: mentre in una distribuzione perfettamente simmetrica media, moda e mediana assumono lo stesso valore, in una distribuzione asimmetrica verso sinistra, come nell’esempio presentato, la media sarà inferiore alla mediana e alla moda.
Il calcolo di media, moda e mediana rappresenta uno dei primi passaggi nella fase di analisi di un set di dati raccolti nel corso di un’investigazione scientifica. Se interpretati con consapevolezza, questi indici supportano il ricercatore nella definizione del migliore approccio analitico e in una corretta interpretazione dei risultati.









