In un precedente articolo abbiamo descritto le caratteristiche che contraddistinguono le variabili categoriche e le principali distribuzioni di probabilità a cui fare riferimento.
Per stimare l’associazione tra due variabili categoriche, è possibile organizzare i dati in quelle che vengono definite tabelle di contingenza, tabelle a doppia entrata nelle quali ciascuna casella indica il valore univoco osservato, incrociando ciascuna modalità di ognuno dei due caratteri considerati. È evidente che la tabella di contingenza avrà una dimensione variabile in relazione al numero di modalità assunte da ciascun carattere. La condizione più semplice è una tabella di contingenza 2 × 2.
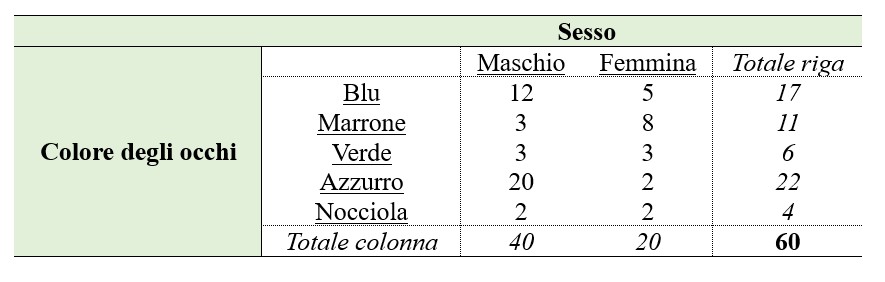
Si prenda ad esempio il caso che si voglia caratterizzare il colore degli occhi in un gruppo di 60 individui, 40 maschi e 20 femmine, distinguendo le osservazioni in base al sesso; in una prima fase si vuole indagare la frequenza con cui si manifesta la modalità “blu” rispetto a una seconda modalità, “non blu”. I risultati vengono tabulati in una tabella di contingenza 2 × 2, con il carattere “sesso” in colonna e il carattere “colore degli occhi” in riga.
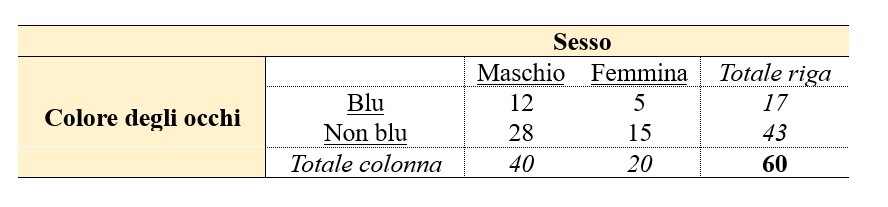
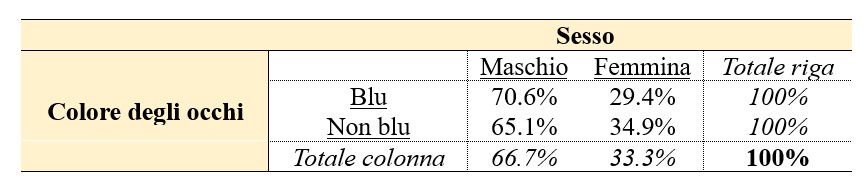
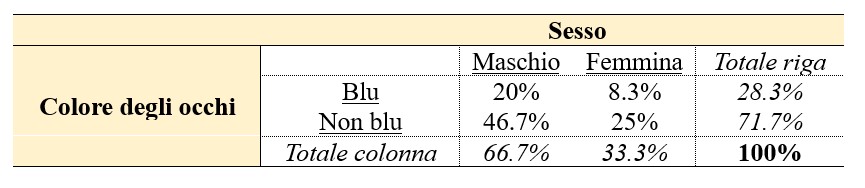
La tabella (1) presenta i conteggi puri, definiti anche frequenze assolute, ottenuti dallo studio. I dati, poi, possono essere espressi in termini di percentuali, calcolate in base al totale di riga (2), al totale di colonna (3) o al totale assoluto (4), con risultati diversi per ciascuna di queste tre condizioni.

Supponendo di estendere l’analisi a molteplici modalità per il carattere “colore degli occhi”, la tabulazione dei conteggi porterà alla costruzione di una tabella di contingenza m × n, come riportato di seguito (5). Anche in questo caso, dalle frequenze assolute sarà possibile ricavare i valori percentuali sulla base del totale di riga, di colonna o il totale assoluto.
Test di indipendenza – χ2
Le tabelle di contingenza possono essere utilizzate non solo per riassumere le frequenze delle osservazioni, ma anche per verificare su base statistica, se tali osservazioni si associano significativamente alle modalità stesse. In particolare, lo sperimentatore può essere interessato a testare l’ipotesi che le due variabili – nell’esempio sopra, “sesso” e “colore degli occhi” – siano indipendenti e cioè che la frequenza con cui si osserva ciascuna modalità del carattere “colore degli occhi” sia indipendente dalle modalità del carattere “sesso”. A questo scopo, è possibile applicare il test χ2 di indipendenza, che testa l’ipotesi nulla (H0) che non ci sia alcuna associazione tra le variabili considerate. Se l’ipotesi nulla viene rifiutata, si rifiuta l’indipendenza tra le stesse.
Il test si basa sul confronto tra frequenze osservate e frequenze attese, queste ultime calcolate su base matematica per ciascuna cella della tabella di contingenza, secondo la formula (Tot. riga × Tot. colonna) / (Tot. assoluto). Se le differenze sono esigue, è probabile che i due caratteri siano indipendenti l’uno dall’altro. A titolo esemplificativo, di seguito sono riportati i calcoli delle frequenze attese per le tabelle di contingenza (1) e (5).

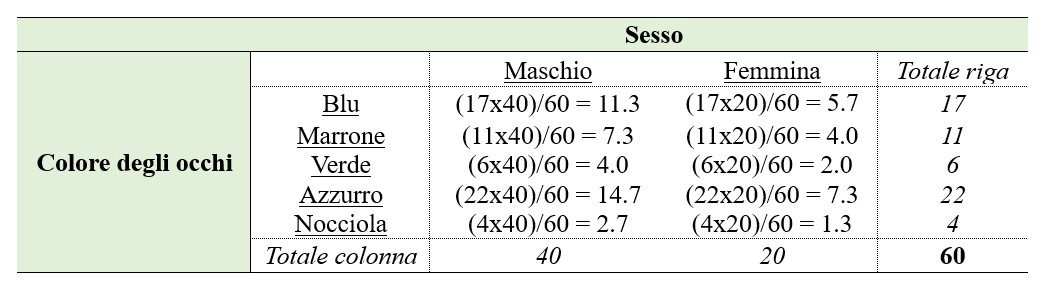
Dal calcolo delle frequenze attese, è possibile ricavare allora il valore di χ2, che si ottiene sommando il quadrato delle differenze tra frequenze osservate e frequenze attese diviso la frequenza attesa nella stessa cella:
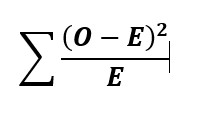
Il valore di χ2 così ottenuto viene confrontato con quelli riportati nella tavola sinottica del χ2; se è maggiore del valore critico tabulato, il test risulterà significativo e si potrà rifiutare l’ipotesi nulla di indipendenza. Il valore critico del χ2 varia in relazione ai gradi di libertà, che si calcolano sulla base del numero di colonne e di righe della tabella di contingenza, secondo la formula (n. righe -1) × (n. colonne – 1).
Nel caso della tabella (1), i gradi di libertà saranno (2-1) × (2-1) = 1; per la tabella (5), saranno (5-1) × (2-1) = 4. Il test effettuato considerando le frequenze delle tabelle (1) e (6) risulta non significativo (χ2 = 0.16; p = 0.69) e indica che non sussiste una relazione statisticamente significativa tra “colore degli occhi” e “sesso”. Il test applicato alle tabelle (5) e (7), invece, è significativo (χ2 = 14.87; p = 0.005), suggerendo che, quando il carattere “colore degli occhi” viene analizzato in relazione a molteplici modalità, è probabile che sussista una dipendenza, non dovuta al caso, rispetto al sesso dei soggetti analizzati.
Quando il test di indipendenza viene effettuato a partire da una tabella di contingenza 2 × 2 e un numero di osservazioni n ≤ 20, è possibile applicare il test esatto di Fisher, che si adatta particolarmente bene a campioni piccoli.
Rischio relativo e odds ratio
Oltre a test statistici specifici, l’associazione tra variabili qualitative può essere espressa anche mediante degli indici, come il rischio relativo (RR) e l’odds ratio (OR). RR è una misura di associazione spesso utilizzata nell’ambito di studi prospettici per verificare se una determinata condizione (ad. esempio “obesità SI” o “obesità NO”) rappresenti un fattore di rischio per il manifestarsi di una malattia (“malattia SI” o “malattia NO”). Si consideri una tabella di contingenza 2 × 2 (8);
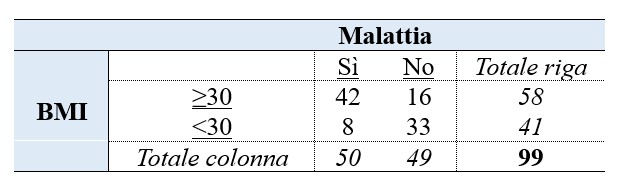
Il rischio che la malattia si manifesti nei soggetti obesi (BMI ≥ 30) è espresso come il rapporto tra i casi di malattia e il totale dei soggetti obesi, cioè 42/58, mentre il manifestarsi della malattia in soggetti non esposti (non obesi) è 8/41. RR è il rapporto tra i due rischi: (42/58) / (8/41) = 3.6. Se RR = 0, non c’è associazione tra la malattia e il fattore di rischio; se RR = 1, il rischio di contrarre la malattia è uguale per tutti i soggetti indipendentemente dal fattore di rischio considerato; se RR > 1, il rischio di contrarre la malattia è maggiore nei soggetti esposti; se RR < 1, il rischio di contrarre la malattia è minore nei soggetti esposti.
L’odds ratio è una misura di associazione che estende il concetto di rischio relativo e che viene utilizzata prevalentemente nell’ambito di studi retrospettivi per analizzare casi e controlli in relazione a un fattore di rischio. Ad esempio, se si analizza la tabella (8), l’odds viene definito come il rapporto tra la probabilità che l’evento (malattia) si verifichi e la probabilità che non si verifichi, cioè (42/58) / (16/58) per i soggetti esposti e (8/41) / (33/41) per i soggetti non esposti. Per calcolare l’OR, allora, si dovrà considerare il rapporto tra gli odds calcolati per i soggetti esposti e quelli non esposti. In pratica, dai valori tabellati, si avrà che OR = [(42/58) / (16/58)] / [(8/41) / (33/41)] = (42/16) / (8/33) = 10.83. In generale, se OR = 0, non c’è associazione tra il fattore di rischio e la malattia; se OR = 1, il rischio di contrarre la malattia è uguale per i soggetti esposti e non; se OR > 1, il rischio di contrarre la malattia è maggiore per i soggetti esposti al fattore di rischio; se OR < 1, il rischio di contrarre la malattia è minore tra i soggetti esposti.
Il test χ2 di indipendenza, il test esatto di Fisher, il calcolo del rischio relativo, degli odds e dell’odds ratio sono solo alcune delle metodologie utilizzate nell’analisi di associazione tra variabili qualitative. Lo sperimentatore dovrà adattarle in relazione al disegno di studio, alla domanda sperimentale e alla natura dei dati raccolti. Questa fase, particolarmente rilevante per la corretta interpretazione dei risultati, può richiedere il supporto di un biostatistico, figura professionale in grado di guidare lo sperimentatore nell’approccio più appropriato.