In generale, in ambito statistico, il termine “regressione” indica la ricerca di un modello matematico che possa descrivere quantitativamente la relazione tra due o più variabili continue misurate sulle unità sperimentali di una (o più) popolazioni di studio. Più in particolare, si parla di “regressione” in quanto si fa riferimento alla tendenza di una variabile a spostarsi, o meglio, a regredire, verso la media qualora sussista una relazione tra i caratteri quantitativi inclusi nel modello.
Più concretamente, uno sperimentatore potrebbe essere interessato a studiare la regressione tra la quantità di luce e l’attività fotosintetica di una pianta; in questo caso la ricerca sarà finalizzata a comprendere la relazione matematica che descriva quantitativamente in che modo le variazioni dell’intensità di luce influenzino l’attività fotosintetica dell’organismo. Questo esempio, pur semplice e molto generico, riassume bene il principio della regressione, evidenziando la necessità di includere nel modello una variabile indipendente (in questo caso l’intensità di luce) e una variabile dipendente (o variabile risposta, in questo caso l’attività fotosintetica). Infatti, il modello matematico definito nell’analisi della regressione è finalizzato a predire come la variabile dipendente (che nel modello corrisponde alla Y) varia in risposta alle variazioni della variabile indipendente (che nel modello viene espressa come la X).
Tornando brevemente all’esempio precedente, la regressione potrà restituire un modello valido per predire come l’attività fotosintetica della pianta si modificherà in risposta a variazioni dell’intensità di luce. Al contrario, cercare di predire le variazioni nell’intensità di luce in risposta a variazioni dell’attività fotosintetica sarebbe decisamente errato: il modello così formulato, infatti, potrebbe portare a concludere che ci si trova in assenza di luce anche se l’attività fotosintetica viene misurata in pieno giorno!
La regressione lineare
L’analisi di regressione fa riferimento a modelli teorici di diversa natura, lineare, parabolico, esponenziale, logaritmico, ecc. Per definire la relazione che intercorre tra le variabili prese in esame, è utile riportare le osservazioni in un grafico definito “scatter plot”, cioè un grafico a dispersione costruito sulla base delle n associazioni tra le variabili e che riporta sulle ascisse i valori assunti dalla variabile indipendente e sulle ordinate i valori assunti dalla variabile dipendente. Sarà possibile così costruire una curva teorica associata a una funzione matematica che rappresenti accuratamente l’andamento decritto dai punti (Figura 1).
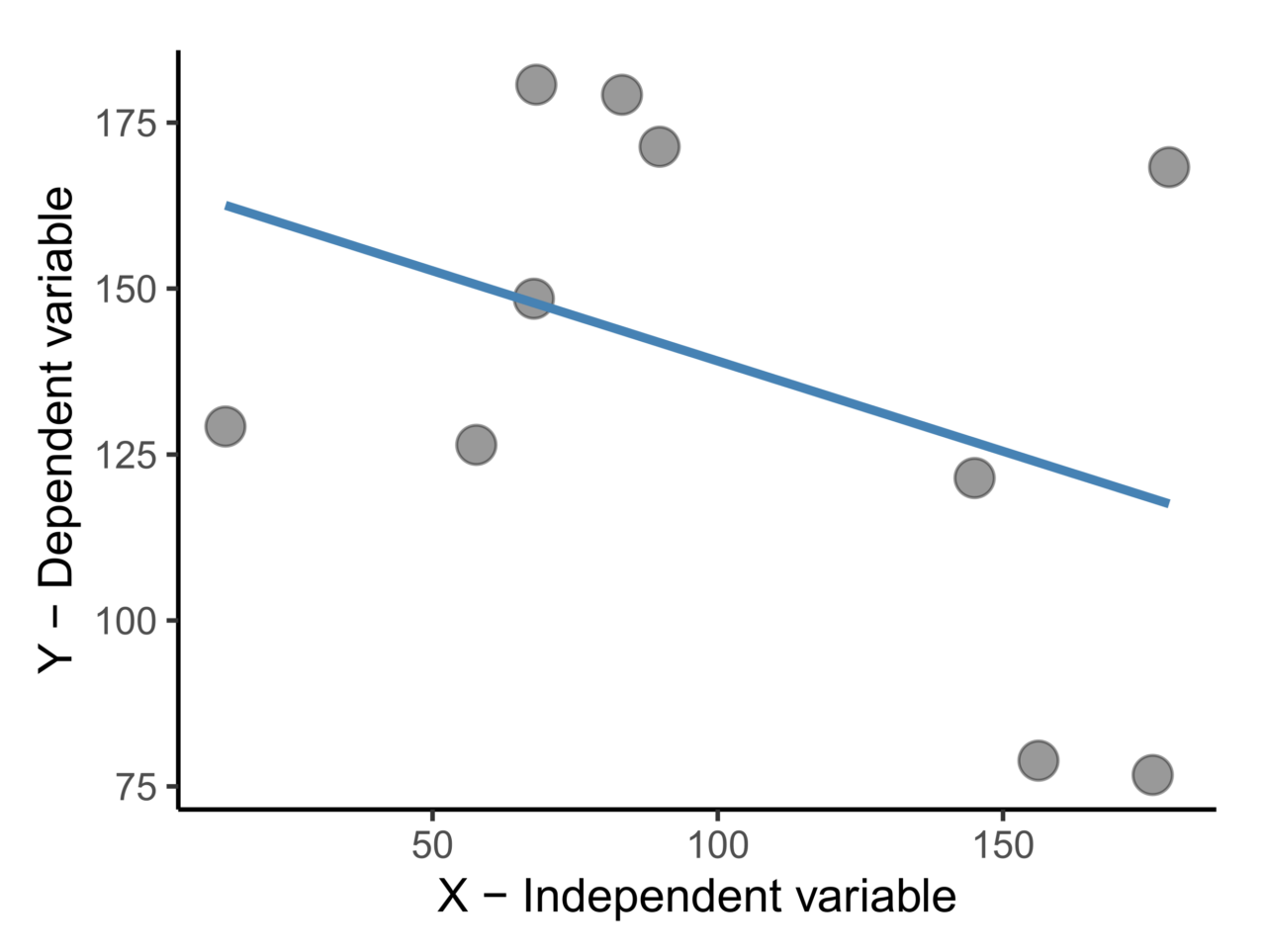
Nel caso dell’analisi di regressione lineare, è possibile modellizzare la relazione causa-effetto che sussiste tra una variabile indipendente (X) e una variabile dipendente (Y) sulla base di una retta di regressione con equazione Y = a + bX, che interpola la nuvola di punti rappresentata nello “scatter plot”. La “a” nell’equazione è definita intercetta sull’asse delle ascisse e corrisponde al valore di Y quando X = 0. La “b” è invece il coefficiente angolare, cioè la pendenza della retta. In base al valore di “b”, si definisce anche il tipo di relazione tra le due variabili prese in esame:
- con b>0, si definisce un’associazione positiva – se la X cresce, cresce anche la Y;
- con b<0, la relazione è negativa – se la X cresce, la Y diminuisce;
- con b=0, non sussiste alcuna relazione tra le variabili.
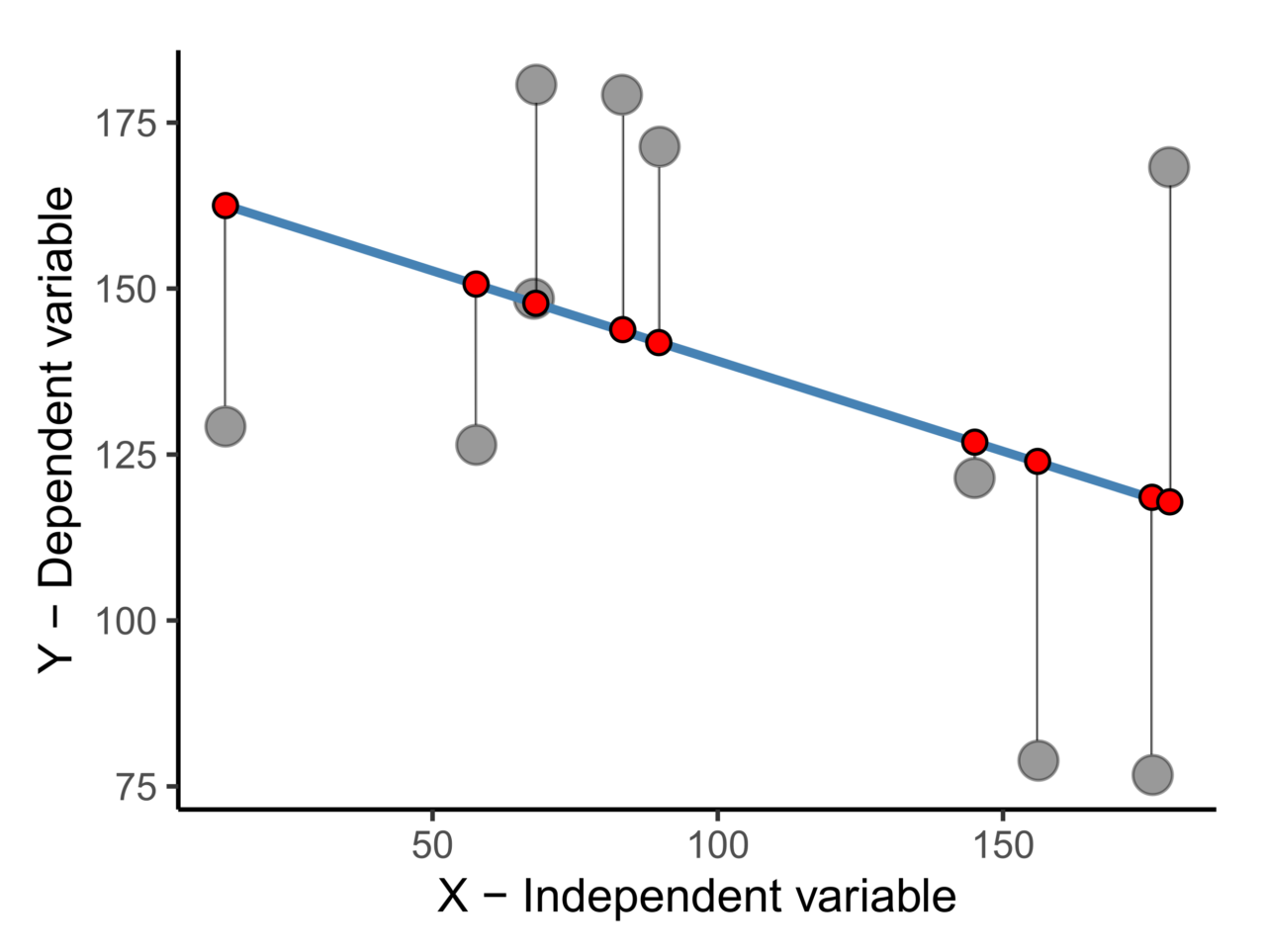
Il metodo utilizzato per stimare la retta di interpolazione – e quindi trovare il modello matematico che sintetizzi la relazione tra X e Y – è quello dei minimi quadrati. Questo approccio permette di definire una retta i cui coefficienti “a” e “b” rendano minima la somma dei quadrati degli scarti tra valori teorici e valori osservati (Figura 2).
La bontà di adattamento tra la retta di regressione e la nuvola di punti viene espressa attraverso un indice univoco, l’indice di determinazione lineare (R2), che assume valori che variano tra 0 e 1.
- Con R2 = 0, la regressione non spiega la relazione che sussiste tra X e Y.
- Con R2 = 1, tutti i punti giacciono sulla retta di regressione.
Se da una parte l’indice di regressione sintetizza la bontà di adattamento della retta interpolante con l’andamento definito dalla nuvola di punti, il coefficiente di correlazione di Bravis-Pearson, definito sulla base della co-varianza, offre una stima della linearità nella relazione tra X e Y. Di fatto, l’indice di Bravis-Pearson r = ± √(R2) e assume valori che variano tra -1 (correlazione inversa) e +1 (correlazione diretta).
L’analisi di regressione è uno strumento utile per definire quantitativamente la relazione tra due variabili continue. Il modello di regressione deve essere costruito con consapevolezza, distinguendo attentamente la variabile dipendente dalla variabile (o dalle variabili) indipendente. Quando è fondato su un chiaro principio di causa-effetto, il modello matematico descritto permette di predire come i valori della variabile dipendente (Y) in risposta a determinati fattori.