In un articolo precedente, è stata presentata l’analisi di regressione, che si definisce come quel metodo statistico utile a predire il valore medio di una variabile dipendente (Y) in risposta a una o più variabili indipendenti (X) – chiamate anche fattori.
Quando le variabili sono caratteri continui, è possibile applicare il modello di regressione lineare. Quale modello di regressione utilizzare, invece, quando la variabile dipendente è un carattere discreto? In tal caso, si ricorre a un modello di regressione di tipo logistico. La regressione logistica può essere di tipo binario, ordinale o multinomiale a seconda delle caratteristiche della variabile dipendente analizzata. Al contrario, la variabile (o le variabili) indipendente può essere costituita da un carattere discreto o da una variabile continua.
Regressione logistica
Si prenda ad esempio un caso in cui gli eventi sperimentali vengano categorizzati come Y = 1 nel caso in cui si sia verificato l’evento di interesse (ad es., presenza di peggioramento delle condizioni di salute) e come Y = 0 se l’evento non sia verificato (ad es., nessun peggioramento). Per valutare la probabilità del verificarsi dell’evento di interesse in relazione a un fattore specifico, è possibile condurre una regressione logistica che stimi la Prob(Y = 1) al variare della variabile indipendente considerata (ad. esempio il sesso dei soggetti, l’età, la dose di un farmaco) (Figura 1).
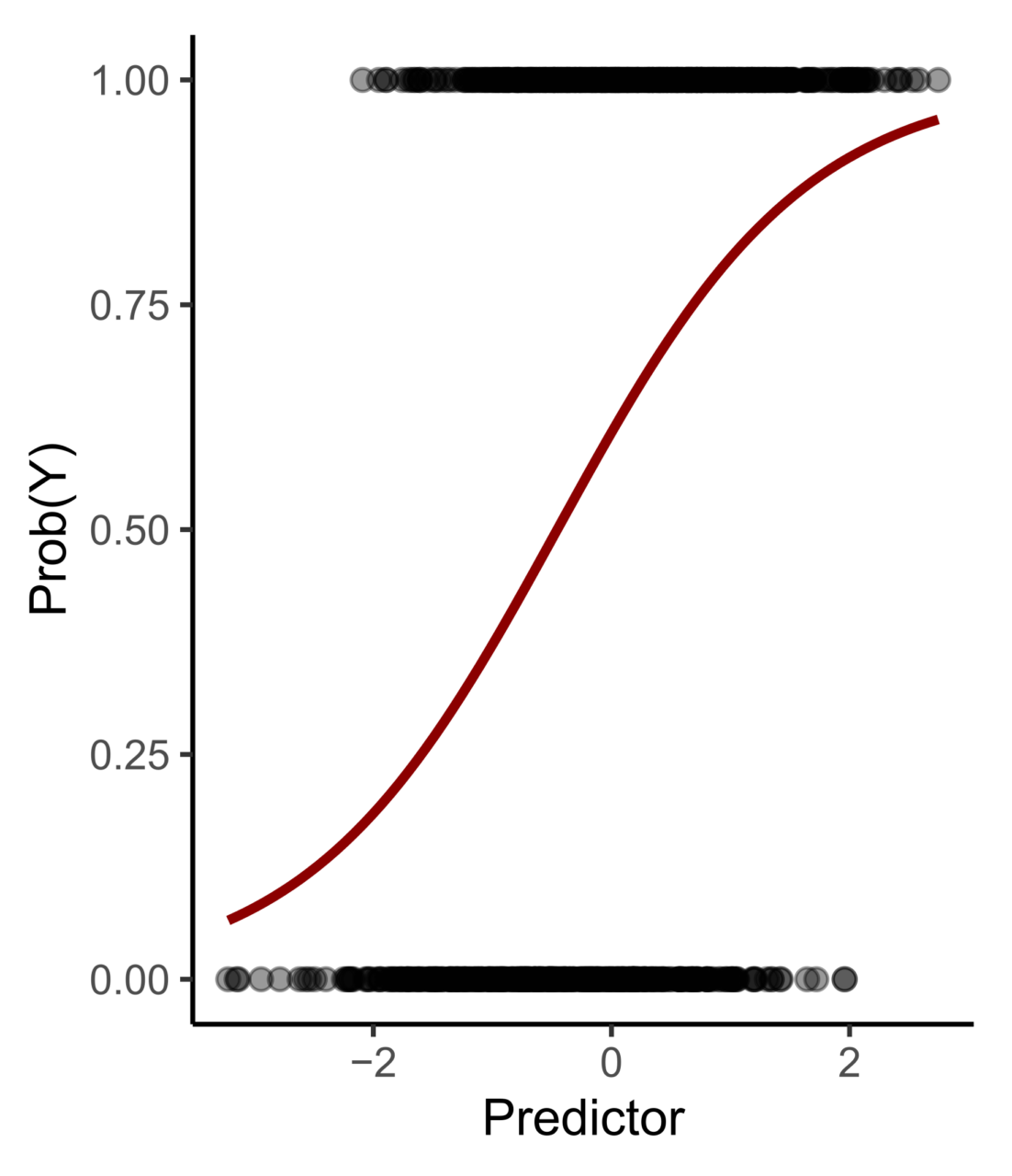
L’equazione che descrive la regressione logistica è del tipo g(.)=β0+β1 x, dove il termine β0+β1 x’ è detto “predittore lineare”, che implica la definizione dell’intercetta β0 e della pendenza β1 di (.). La funzione (.) è detta “link function” e assicura che tutti i valori stimati dal predittore lineare siano sempre compresi nell’intervallo [0,1]. In tal modo,
se il predittore lineare diminuisce, la Prob(Y) tende a 0;
se il predittore lineare aumenta, la Prob(Y) tende a 1 (Figura 2).
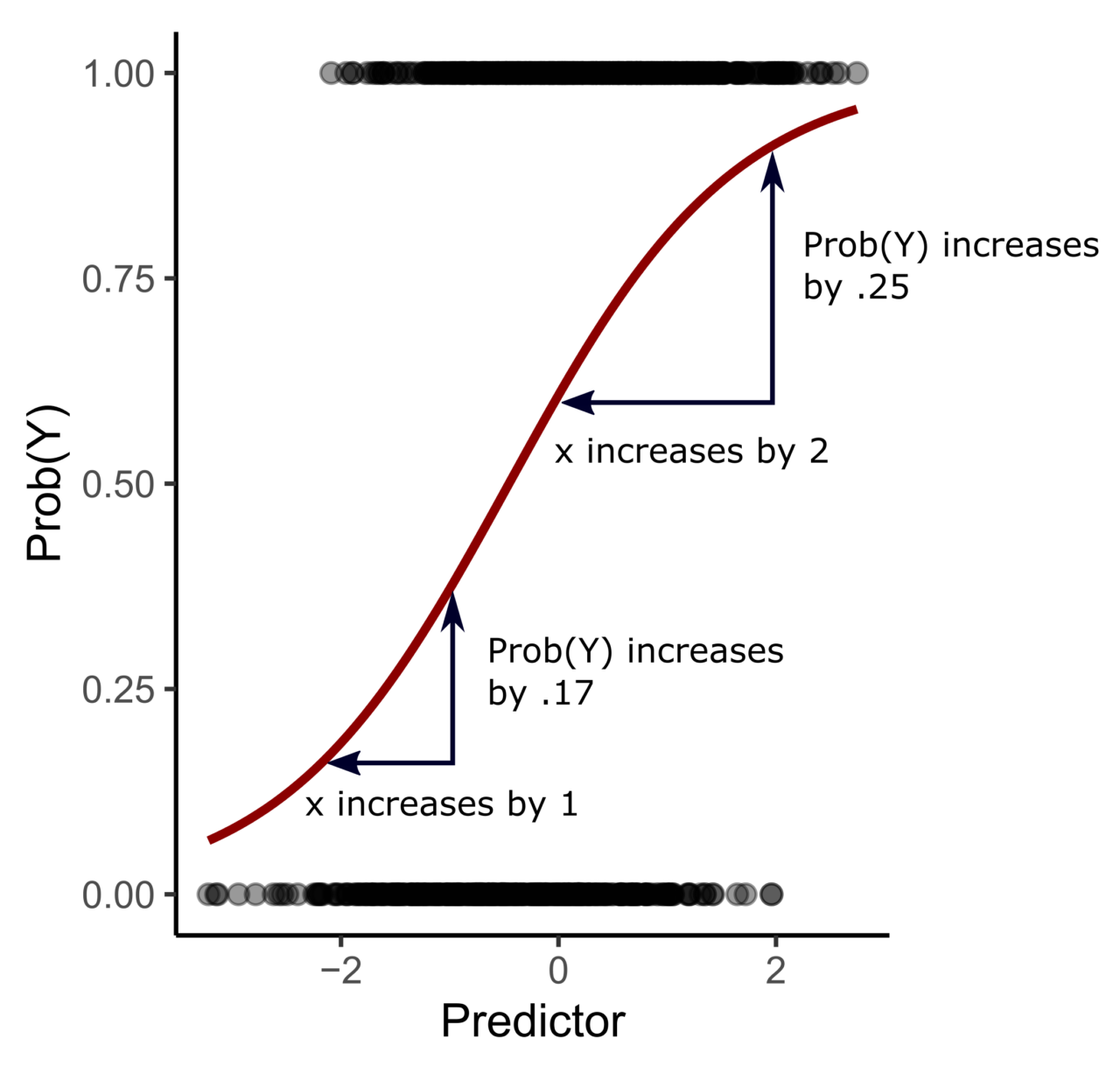
Nella regressione logistica, la funzione (.) è definita “logit” e corrisponde al logaritmo dell’odds dell’evento di interesse:
Da queste considerazioni sulla struttura del modello di regressione logistica, si traggono le seguenti conclusioni in relazione al valore assunto dalla funzione logit.
Se Prob(Y) = 0.5, allora l’Odds = 0.5/(1-0.5) = 1; allora logit = log(1) = 0
Se Prob(Y) > 0.5, allora l’Odds > 1; allora logit > 0
Se Prob(Y) < 0.5, allora l’Odds < 1; allora logit < 0
Quando la variabile risposta è costituita da un carattere discreto ordinale, la regressione logistica viene adattata di conseguenza. Infatti, la variabile risposta non assumerà più un valore dicotomico (1 o 0), ma piuttosto n valori arbitrari ordinati, in modo che gli n eventi siano mutualmente esclusivi, così che Y = 1 < 2 < 3 < 4 < … < k. Il modello definisce la probabilità di ciascun evento utilizzando una trasformazione della funzione logit:
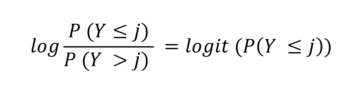
In questo modo, si costruisce un modello per odds proporzionali, che includerà un numero di coefficienti β0 (intercette) pari al numero di livelli k-1 e un numero di coefficienti β pari al numero di confronti. Si prenda ad esempio il caso in cui si voglia testare la soddisfazione dei pazienti rispetto a 3 possibili terapie (1, 2 o 3), in relazione alle quali ogni soggetto ha espresso un giudizio di gradimento (“scarso”, “sufficiente”, “buono”, “ottimo”, “eccellente”). In questo caso, il numero di intercette sarà pari al numero di livelli k-1 = 5-1 = 4. Il numero di confronti, invece, sarà pari al numero di terapie meno uno = 3-1 = 2. In base ai valori di β0 e β sarà possibile definire quale terapia sarà stata maggiormente preferita dai pazienti.
La regressione logistica è un metodo statistico che permette di stimare l’influenza di fattori continui e/o discreti su una variabile categorica, sia essa dicotomica, ordinale o multinomiale. In questo modo, è possibile inferire con quale probabilità Prob(Y) si possa verificare un evento in risposta ai predittori inclusi nel modello.