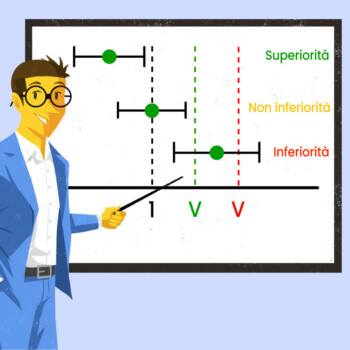
Rispetto alle statistiche applicate a variabili continue, quelle utilizzate per l’analisi di caratteri qualitativi presentano delle peculiarità dovute alla natura dei dati e alle distribuzioni di probabilità. Le analisi descrittive si basano su conteggi e percentuali e la statistica inferenziale ha delle proprietà a sé stanti. È utile ricordare che la statistica inferenziale è quel processo che consente di identificare i parametri dell’intera popolazione teorica a partire dalle informazioni campionarie; date le diverse distribuzioni di probabilità applicabili ai dati qualitativi, anche i metodi statistici inferenziali saranno diversi rispetto a quelli utilizzati per le variabili continue.
Dati categorici – caratteristiche
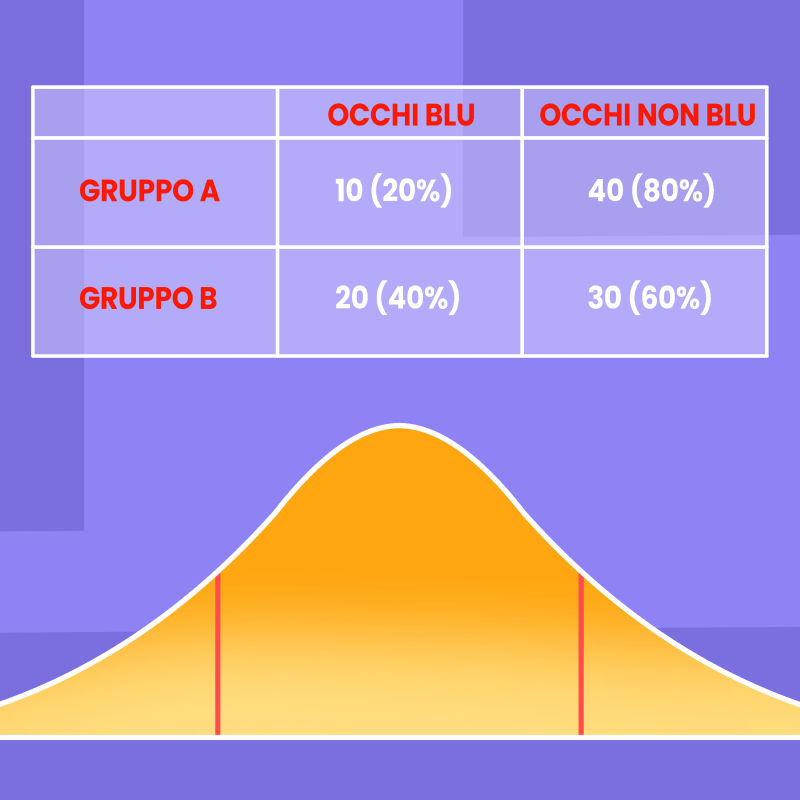
Le variabili di tipo categorico si basano sull’assegnazione di un conteggio o una percentuale alle modalità di un carattere, i cui livelli possono essere ordinati o meno. Ad esempio, si può contare quante volte si osserva il carattere “blu” nell’analisi del colore degli occhi di un gruppo di persone, per poi calcolarne la percentuale. In questo esempio banale, il carattere “colore degli occhi” presenta il livello (“blu”) che si contrappone a un altro livello, “non blu”. Allo stesso carattere possono essere assegnati anche più livelli (“blu”, “verde”, “marrone”, “azzurro”). Questo esempio può essere esteso a caratteri di diverso tipo; principalmente, si distinguono caratteri nominali (ad es. nazionalità, etnia, sesso), ordinali (ad es. la scala Likert) e intervallari (ad es. le fasce di età, le fasce di reddito). I primi mancano di un preciso ordine logico, i caratteri ordinali sono ordinabili, appunto, secondo un ordine logico naturale (ad es. da scarso a ottimo) e i caratteri intervallari consistono in valori raggruppati per categorie definite sulla base di intervalli numerici.
Una variabile categorica viene classificata in base alla scala di misura del carattere. Se si considera un carattere binario (cioè che include solo due livelli, come “0”, “1” oppure “sì”, “no”), la variabile viene classificata come bernoulliana qualora sia stata ottenuta da una singola prova e binomiale se le occorrenze vengono misurate su n prove, con n > 1. Ad esempio, può essere analizzato il carattere “colore degli occhi” e considerati due livelli, “blu” e “non blu”. Se questo carattere viene analizzato su un singolo individuo, la variabile categorica è di tipo bernoulliano. Se invece l’analisi viene effettuata su un gruppo di individui definito, la variabile viene classificata come binomiale. Quando si analizza un carattere con un numero di livelli k superiore a 2 (k > 2), la variabile categorica viene classificata come multinomiale.
Dati categorici – principali distribuzioni di probabilità
In relazione alla classificazione della variabile categorica e alle caratteristiche del disegno sperimentale, variano anche le distribuzioni di riferimento per l’analisi inferenziale. Le distribuzioni di probabilità usate più comunemente nella statistica inferenziale applicata a variabili categoriche sono la distribuzione di Bernoulli, binomiale, di Poisson, multinomiale e ipergeometrica.
Una variabile casuale di tipo bernoulliano può assumere due soli valori e la rispettiva distribuzione di probabilità, la distribuzione di Bernoulli, descrive un esperimento in cui sono possibili due esiti (ad es. “successo” o “insuccesso”), con frequenza complementare.
La distribuzione binomiale può essere considerata un’estensione della distribuzione di Bernoulli. È la distribuzione di riferimento per campionamenti della variabile su n prove bernoulliane che siano tra loro indipendenti (il risultato delle prove non viene influenzato da quelle precedenti) e identiche (ogni prova preserva la stessa probabilità di occorrenza), misurando quante volte l’evento (ad es. “successo” o “insuccesso”) si verifica nell’ambito di queste n prove prefissate. La distribuzione binomiale, quindi, è quella di riferimento quando il carattere misurato presenta due soli livelli (“1”, “0”; “sì”, “no”; “successo”, “insuccesso”; “maschio”, “femmina”, ecc.) e il numero di prove è prefissato. Quindi, il numero di eventi (ad es. il successo) è limitato al numero n di prove (evento ≤ n).
Mentre nella distribuzione binomiale la dimensione campionaria (n) è data dalle n prove, nella distribuzione di Poisson la dimensione campionaria è data dal numero di unità o intervalli spaziali/temporali all’interno dei quali si misurano le occorrenze di un evento. In questo caso, quindi, non si pone alcun limite al numero di occorrenze che si possono verificare – e che si misurano – in quell’intervallo di tempo o in quello spazio. Anche la distribuzione di Poisson si basa su un numero n prefissato, ma rispetto alla binomiale cambia la distribuzione di probabilità delle occorrenze.
Uno degli assunti fondamentali per fare riferimento alla distribuzione di probabilità binomiale è che il numero di prove n sia fisso. Se questa condizione non viene rispettata, sarà diversa anche la distribuzione di probabilità di riferimento. Ad esempio, se la variabile categorica viene misurata su campioni senza reimmissione, la probabilità di occorrenza varierà per ogni prova effettuata e la distribuzione di riferimento sarà quella ipergeometrica. L’esempio più eclatante è quello dell’estrazione dei numeri del lotto; mentre alla prima estrazione la probabilità di ottenere il numero 3 è di 1/90, alla seconda estrazione la probabilità è di 1/89 e così via. Nel campionamento senza reimmissione, quindi, le occorrenze si valutano su una dimensione campionaria variabile, generando una distribuzione di probabilità dedicata.
La distribuzione multinomiale, infine, è un’ulteriore estensione del modello binomiale e si distingue per il fatto che i possibili esiti (cioè i livelli di un carattere) in ciascuna prova sperimentale sono k > 2. Se le n prove sono identiche e indipendenti, allora si fa riferimento a una distribuzione multinomiale. È evidente che con k > 2 l’occorrenza può essere assegnata a un singolo esito k, escludendo automaticamente l’occorrenza nelle altre modalità della variabile categorica.
In conclusione
La natura della variabile categorica e il disegno sperimentale influenzano fortemente la distribuzione di probabilità di riferimento nell’ambito della statistica inferenziale. È necessario che lo sperimentatore valuti con attenzione queste caratteristiche per poter pervenire a conclusioni accurate.