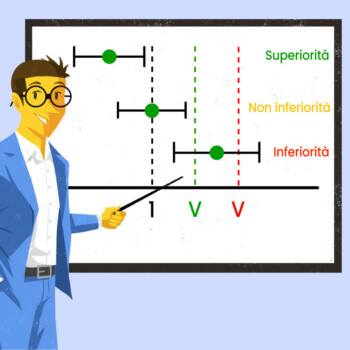
La definizione del livello di significatività statistica è un passaggio fondamentale per determinare quantitativamente la probabilità che sussistano differenze tra gruppi sperimentali in virtù di un trattamento – o una condizione – che influenza la variabile casuale misurata. Solitamente il livello di significatività viene fissato al 5%. Ciò significa che lo sperimentatore accetta un’uguale probabilità di commettere un errore statistico di tipo I, con implicazioni pratiche nel processo di inferenza statistica. Ma facciamo un passo indietro e andiamo per gradi.
La significatività statistica ricopre un ruolo chiave nell’interpretazione dei test di ipotesi, infatti, in relazione alla significatività del test statistico, lo sperimentatore decide se rifiutare o meno l’ipotesi nulla a favore dell’ipotesi alternativa. A questo scopo, è necessario identificare una soglia di probabilità rispetto alla quale poter interpretare il risultato del test come significativo. Per convenzione, questa soglia viene posta pari al 5%.
Ma perché spesso si fa riferimento a questo valore? Qual è la ragione dietro questa convenzione? Per rispondere a queste domande, è necessario richiamare la teoria della probabilità. La probabilità è una misura della possibilità che un evento si verifichi. Quando questo concetto viene applicato alla statistica, ci consente di trarre conclusioni sulla popolazione statistica di riferimento attraverso un processo inferenziale basato sulle stime campionarie. A questo scopo, i test statistici supportano lo sperimentatore nel determinare se le misure raccolte afferiscano a una stessa popolazione statistica o se sussistano delle disparità tali da portare a concludere che le misure derivano da popolazioni distinte.
Considerando che la stima dei parametri della popolazione avviene su base campionaria e che le misure campionarie sono soggette alle leggi del caso, l’inferenza statistica è per sua natura associata a una probabilità di errore, che lo sperimentatore è interessato a quantificare per comprendere la solidità delle conclusioni a cui perviene. In particolare, si distinguono due tipi di errore statistico: l’errore di tipo I (α) e l’errore di tipo II (β). Il primo si verifica quando l’ipotesi nulla, vera, viene rigettata. L’errore di tipo II si verifica, invece, quando si accetta erroneamente un’ipotesi nulla falsa. Nel contesto dei test statistici, il livello di significatività è il massimo tasso di errore di tipo I che lo sperimentatore è disposto a tollerare e il 5% è spesso scelto come livello di significatività d’elezione. Va detto che questo valore è a totale discrezione dello sperimentatore, ma una soglia del 5% rappresenta un compromesso ragionevole tra due esigenze conflittuali; da un lato, quella di minimizzare la probabilità di commettere un errore di tipo I, dall’altro quella di massimizzare la potenza del test per far sì di rilevare un effetto quando questo effettivamente sussiste – a tale proposito, infatti, va ricordato che la potenza di un test statistico (definita come 1-β) è intrinsecamente legata alla probabilità di errore di tipo II. Riducendo il livello di significatività α (considerando cioè un valore inferiore al 5%), si riduce la probabilità di errore di tipo I, ma aumenta la probabilità di commettere un errore di tipo II. Al contrario, aumentando α, diminuisce la probabilità di commettere un errore di tipo II (con una maggiore potenza del test), ma aumenta la probabilità di commettere un errore di tipo I. Il livello del 5% è quindi un compromesso che fornisce un equilibrio tra queste due esigenze, comportando sì una probabilità del 5% di respingere erroneamente un’ipotesi nulla vera, ma anche una probabilità del 95% di non commettere questo errore. Questo livello di probabilità è generalmente considerato accettabile in molte discipline scientifiche.
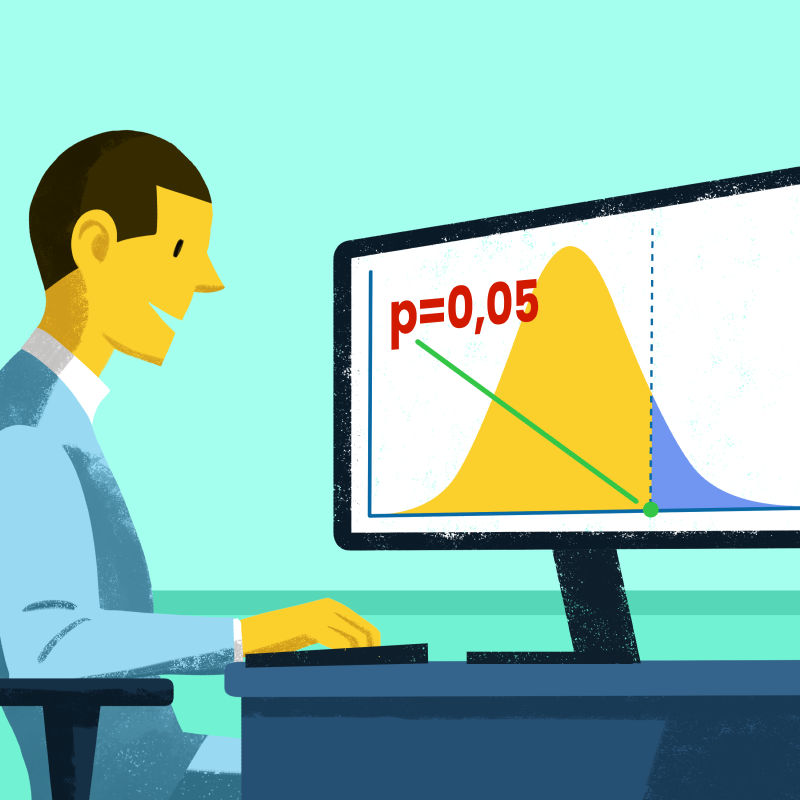
Dopo aver fissato una soglia di significatività, il passaggio successivo per quantificare l’errore è legato al concetto di p-value. Questo valore esprime la probabilità di osservare un risultato almeno altrettanto estremo di quello effettivamente osservato, assumendo che l’ipotesi nulla sia vera. Se il p-value è inferiore al livello di significatività scelto (ad esempio, 5%), allora è possibile decidere di rigettare l’ipotesi nulla. Tuttavia, è importante ricordare che la significatività statistica non implica necessariamente importanza pratica o rilevanza clinica. Pertanto, è essenziale valutare anche l’entità dell’effetto e la sua importanza nel contesto specifico.
Il livello di significatività del 5% rappresenta un compromesso equilibrato tra il rischio di commettere un errore statistico di tipo I o di tipo II. Questa convenzione, fondata sulla teoria della probabilità, fornisce una base solida per l’interpretazione dei risultati. Tuttavia, è essenziale valutare attentamente anche l’entità dell’effetto e l’importanza pratica dei risultati, al di là della significatività statistica.